2014-02-02
863
Теоремы Z-преобразований.
1). Линейность Z-преобразований
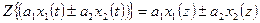(3.11)
2). Теорема о начальном значении аргумента оригинала
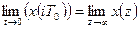(3.12)
3). Теорема о конечном значении оригинала
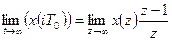(3.13)
4). Теорема о смещении
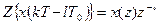(3.14)
Z-k означает значение функции в момент времени (t-kT0)
·.Чтобы получить прямое дискретное преобразование Лапласа сигнала x(t), необходимо заменить этот сигнал дискретными значениями x(kT0). Каждое значение x(kT0) помножить на z-k, а затем полученный степенной ряд свернуть в конечную сумму, которая представляет собой дискретное преобразование Лапласа x(z). Прямое z -преобразование является однозначным преобразованием непрерывного сигнала в дискретный..
· Чтобы по известному изображению x(z) получить сигнал x(t), необходимо представить изображение x(z) в виде степенного ряда, числовые значения коэффициентов при степенях z-k, которого и есть изображение x(kT0). Этот этап также является однозначным.
· Переход x(kT0)® x(t) является неоднозначным, так как неизвестно поведение функции в промежутках между замыканием ключей.
