Решетчатая функция – функция, которую образуют ординаты непрерывной функции при дискретных равноотстоящих друг от друга значениях независимой переменной. Решетчатая функция существует только при дискретных значениях аргумента. То есть для описания импульсной системы с амплитудной модуляцией наилучшим образом подходит решетчатая функция. При этом непрерывный сигнал 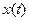 импульсным элементом преобразуется в последовательность импульсов
импульсным элементом преобразуется в последовательность импульсов  , то есть в решетчатую функцию. Непрерывная функция
, то есть в решетчатую функцию. Непрерывная функция 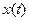 является огибающей для решетчатой функции
является огибающей для решетчатой функции 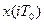 . Введем понятие единичного импульса
. Введем понятие единичного импульса 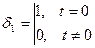 , тогда последовательность неединичных импульсов может быть представлена в следующем виде:
, тогда последовательность неединичных импульсов может быть представлена в следующем виде:
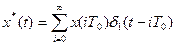 (3.6)
(3.6)
Изображение Лапласа для i-того неединичного импульса имеет вид:
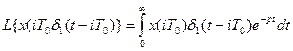 (3.7)
(3.7)
Так как для каждого фиксированного значения i величина 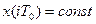 , то ее можно вынести за знак интеграла. Согласно теореме запаздывания изображение смещенной
, то ее можно вынести за знак интеграла. Согласно теореме запаздывания изображение смещенной 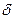 -функции равно
-функции равно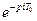 . Тогда выражение (7) можно переписать:
. Тогда выражение (7) можно переписать:
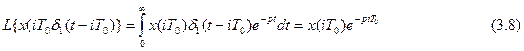
Тогда изображение по Лапласу всей последовательности импульсов равно:

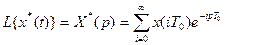 (3.9)
(3.9)
Выражение (9) называется дискретным преобразованием Лапласа. Оно устанавливает соответствие между решетчатыми функциями и их изображениями. Введя новую перемену. 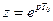 , можно получить так называемое z-преобразование:
, можно получить так называемое z-преобразование:
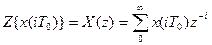 (3.10)
(3.10)
Таким образом, математически преобразование непрерывного сигнала в дискретный сигнал осуществляется следующим образом:
1. непрерывный сигнал 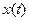 заменяется последовательностью импульсов
заменяется последовательностью импульсов 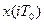 (решетчатая функция).
(решетчатая функция).
2. к решетчатой функции 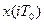 применяется z-преобразование
применяется z-преобразование 
3. степенной ряд сворачивается в конечную сумму. Это конечная сумма и представляет собой дискретные преобразования Лапласа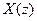 .
.
Пример
Получить Z- преобразование функции 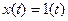 .
.
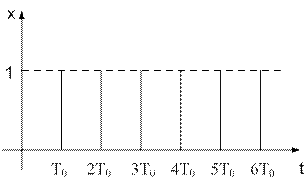
Рис. 3.11.
1. Решетчатая функция имеет вид 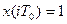
2. 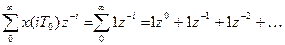
3. Конечная сумма ряда: 
Для большинства встречающихся в задачах решетчатых функций z-преобразование может быть выполнено при помощи таблиц соответствия, которые приводятся в специальной литературе по импульсным системам.
Простейшая таблица дискретных преобразований
| x(t) | x(p) | x(z) |
| d(t) | ||
| d(t-iT) | 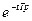 | 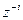 |
| 1(t) | 1/p | 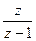 |
| T | 1/p2 | 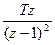 |
| T2 | 2!/p3 | 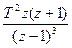 |
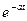 | 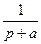 | 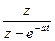 |
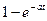 | 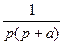 | 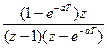 |
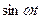 | 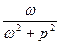 |  |
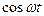 | 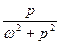 | 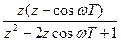 |
Свойства z -преобразования аналогичны свойствам обычного преобразования. Приведем важнейшие из них.
 2014-02-02
2014-02-02 8632
8632








