Метод фазовых траекторий

Исследование режима автоколебания.

Для исследования режима автоколебаний существует несколько методов, Самые распространенные методы – это метод фазовых траекторий и метод гармонический линеаризации.

Метод фазовых траекторий представляет собой графо-аналитический способ исследования нелинейных систем. Сущность метода заключается в описании поведения системы при помощи наглядных геометрических представлений – фазовых портретов.

Динамика нелинейных систем с выходной переменной 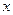в общем случае описывается с помощью нелинейного дифференциального уравнения:

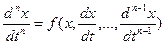(4.15)

Данное уравнение можно представить в виде системы нелинейных дифференциальных уравнений первого порядка:

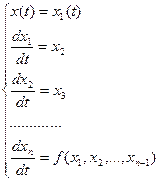(4.16)

Переменные 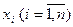называются фазовыми переменными состояния. Мгновенное состояние системы и ее дальнейшее поведение однозначно определено, если в некоторый момент времени 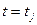известны значения всех 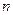переменных 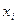. Эти значения можно рассматривать как координаты точек 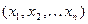в n- мерном пространстве, которое называется фазовым пространством.

Точку с координатами 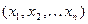называют изображающей точкой, а линию, по которой она перемещается при изменении состояния системы – фазовой траекторией. Известно, что конкретному начальному состоянию системы 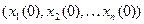соответствует единственное решение системы (4.16), а следовательно единственная фазовая траектория. Поэтому множеству различных начальных условий соответствует семейство фазовых траекторий, которое называется фазовым портретом. Построение фазового портрета дает нагляднее представление о поведении системы, в том числе предоставляет возможность определить режим автоколебаний.

Метод фазового пространства наиболее удобен для анализа систем второго порядка, так как их фазовые траектории располагаются в одной плоскости – в фазовой плоскости переменных x₁ и x₂. Фазовый портрет этих систем можно построить непосредственно по дифференциальному уравнению, не решая его.

Пусть описание системы представлено в виде дифференциального уравнения второго порядка:

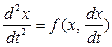(4.17)

Данное уравнение можно представить в виде системы двух дифференциальных уравнений первого порядка

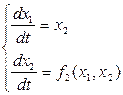, (4.18)

где 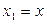- отклонение выходной величины от установившегося значения. В качестве переменной 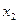принята производная переменной 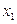: 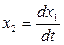. Разделив второе уравнение системы (4.18) на первое, можно получить уравнение фазовых траекторий в дифференциальной форме:

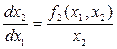(4.19)

Решение данного дифференциального уравнения имеет уравнения фазовых траекторий в явном виде:

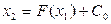, (4.20)

где 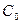- постоянная интегрирования, зависящая от начальных условий.

ПРИМЕР

Рассмотрим колебательное звено (систему второго порядка):

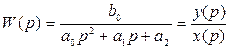(4.21)

Вывести уравнение фазовой траектории.

Дифференциальное уравнение, соответствующее данному звену имеет вид:

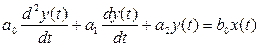(4.22)

Данное дифференциальное уравнение может быть представлено в виде системы уравнений:

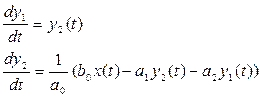, (4.23)

где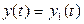

Разделив второе уравнение системы на первое, получаем уравнение фазовых траекторий в дифференциальной форме:

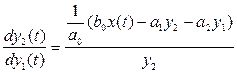(4.24)

Метод фазовых траекторий удобно применять, если объект управления описание в терминах пространства состояния.