Звено имеет неколебательный (апериодический) характер переходного процесса и описывается дифференциальным уравнением первого порядка вида
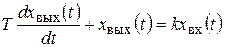 , (3.6)
, (3.6)
где k – коэффициент передачи, характеризующий свойства в статическом режиме; Т – постоянная времени, характеризующая инерционность звена.
Решение уравнения (3.6) при нулевых начальных условиях (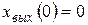 ;
;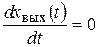 ) имеет вид
) имеет вид
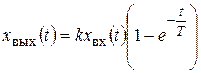 . (3.7)
. (3.7)
При однократном ступенчатом воздействии х вх(t) = const получим динамическую характеристику звена в виде кривой разгона (разгонной характеристики). Простейший анализ уравнения (3.7) показывает что при t = 0 имеем 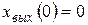 , а при t ® ¥ выходная величина х вых(¥) = kх вх(¥), изменяясь по экспоненте, устанавливается на новом значении (рис. 3.3).
, а при t ® ¥ выходная величина х вых(¥) = kх вх(¥), изменяясь по экспоненте, устанавливается на новом значении (рис. 3.3).
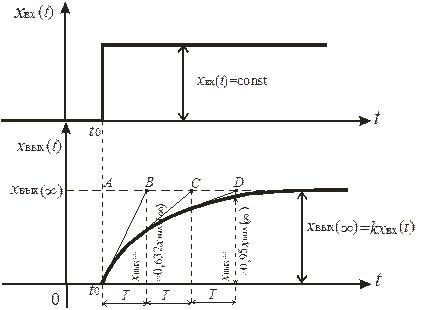
| Рис. 3.3. Кривая разгона апериодического звена первого порядка |
Из анализа уравнения (3.7) следуют свойства экспоненты, широко используемые на практике:
1) проекция на ось времени отрезка касательной, заключенного между точкой касания и линией установившегося значения параметра х вых(¥), есть величина постоянная для данной экспоненты и равная постоянной времени Т (рис. 3.3);
|
|
|
2) касательная, проведенная к кривой разгона в начальной точке t = 0 (при t 0 = 0), отсекает на горизонтальной прямой х вых(¥) = const отрезок АВ, численно равный постоянной времени Т. Значение выходного параметра в конце отсчета постоянной времени (по линии проекции точки В на ось времени) равно х вых(t) = 0,632 х вых(¥) – рис.3.3;
3) если отложить последовательно друг за другом три постоянных времени Т (t = 3 Т), то значение выходного параметра при t = 3 Т составит х вых(t) = 0,95 х вых(¥), т.е. можно считать, что переходный процесс практически закончился (рис. 3.3).
Передаточная функция звена получается из записи уравнения в операторной форме:
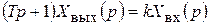 ;
;
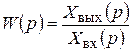
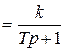 . (3.8)
. (3.8)
Частотные характеристики звена получаются из представления частотной передаточной функции звена в виде комплексного числа при замене в (3.8) р значением j w:
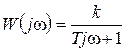 . (3.9)
. (3.9)
Умножая числитель и знаменатель функции (3.9) на выражение, сопряженное со знаменателем, можно избавиться от величины j в знаменателе и представить амплитудно-фазовую характеристику в виде суммы действительной и мнимой частей:
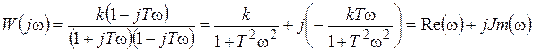 . (3.10)
. (3.10)
Амплитудно-частотная характеристика звена равна

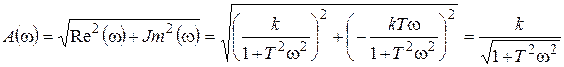 . (3.11)
. (3.11)
При изменении частоты w от 0 до ¥ амплитудно-частотная характеристика изменяется от k (при w = 0) до 0 (при w = ¥), что показано на рис 3.4.
| Рис. 3.4. Амплитудно-частотная характеристика апериодического звена первого порядка |
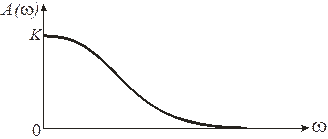
Из рис 3.4 следует: гармонические сигналы малой частоты пропускаются звеном хорошо (отношение амплитуд выходных и входных колебаний близко к передаточному коэффициенту k). Сигналы большой частоты плохо пропускаются звеном: отношение амплитуд существенно меньше коэффициента передачи k.
|
|
|
Таким образом, апериодическое (инерционное) звено первого порядка по своим частотным свойствам является фильтром низких частот. Чем больше постоянная времени Т, тем больше инерционность звена и тем уже полоса пропускания.
Фазочастотная характеристика звена равна:
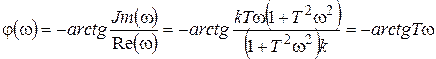 , (3.12)
, (3.12)
т.е. происходит отставание по фазе выходной величины по отношению к входной.
| Рис. 3.5 Фазочастотная характеристика апериодического звена первого порядка |
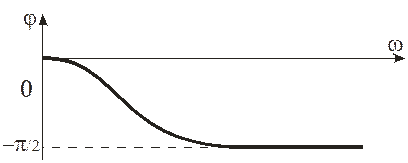
При изменении частоты от 0 до ¥ (рис. 3.5) отставание по фазе происходит от j(0) = arctg 0 = 0 до j(¥) = – arctg ¥ = –p/2.
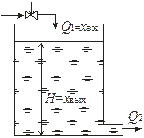
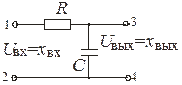
Примерами апериодических звеньев первого порядка могут быть: бак с водой, входной величиной которого является приток жидкости х вх = Q 1, а выходной – уровень жидкости х вых = Н (рис. 3.6, а); емкость для сглаживания давления воздуха, входной величиной которой является приток воздуха х вх = Q 1, а выходной – изменение давления Р 2 в емкости х вых = Р 2 (рис. 3.6, б); электрическая цепь, содержащая сопротивление R и конденсатор с электрической емкостью С, входной величиной которой является напряжение, приложенное к точкам 1 – 2, а выходной – напряжение, снимаемое с точек 3 – 4 (рис. 3.6, в).
 | 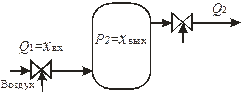 |  |
| а | б | в |
| Рис. 3.6. Примеры апериодических звеньев первого порядка |
Инерционными звеньями первого порядка являются конструктивные элементы, которые могут накапливать и передавать энергию или вещество. В гидравлических элементах накопителем вещества является объем бака, в пневматических – емкость (объем) резервуара; в электрических – накопителем электрического тока служит емкость конденсатора.
 2014-02-02
2014-02-02 33524
33524








