Упрощенный способ вычисления
Вычисление числовых характеристик выборки
Таблица 6
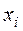 | 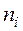 | 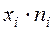 | 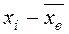 | 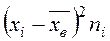 | 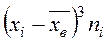 | 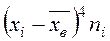 |
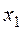 |  | |||||
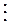 | 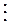 | |||||
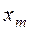 | 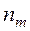 | |||||
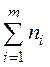 | 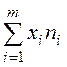 | 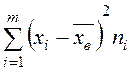 | 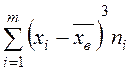 | 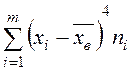 |
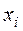 - середины интервалов;
- середины интервалов; 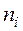 - частоты;
- частоты; 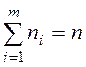 - объем выборки;
- объем выборки;
с помощью суммы 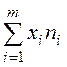 находим
находим 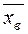 ;
;
с помощью суммы 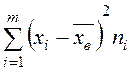 находим
находим 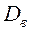 и
и 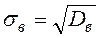 ;
;
с помощью суммы 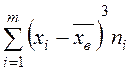 находим
находим 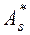 ;
;
с помощью суммы 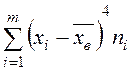 находим
находим 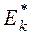 .
.
При больших значениях вариантов и соответствующих им частот вычисление выборочного среднего, дисперсии и выборочных моментов по приведенным ниже формулам приводит к громоздким вычислениям.
В этом случае используют условные варианты 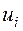 , определяемые по формулам:
, определяемые по формулам: 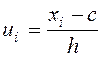 , где числа
, где числа 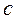 и
и 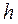 выбираются произвольно.
выбираются произвольно.
Чтобы упростить вычисления в качестве 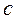 выбирают вариант, который имеет наибольшую частоту или находится в середине ряда. Число
выбирают вариант, который имеет наибольшую частоту или находится в середине ряда. Число 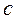 называется «ложным нулем». В качестве
называется «ложным нулем». В качестве 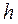 выбирают число равное длине интервала (в случае интервального ряда) или наибольший общий делитель разностей
выбирают число равное длине интервала (в случае интервального ряда) или наибольший общий делитель разностей 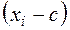 .
.
Для вычисления числовых характеристик выборки составляем табл. 7.
Таблица 7.
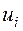 | 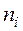 | 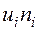 | 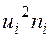 | 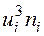 | 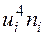 | 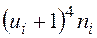 |
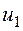 |  | |||||
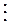 | 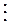 | |||||
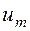 | 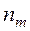 | |||||
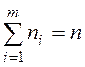 | 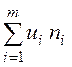 | 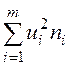 | 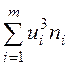 | 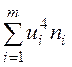 | 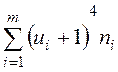 |
Контроль:

С помощью сумм, полученных в нижней строке таблицы, находим условные моменты:
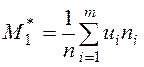 ,
, 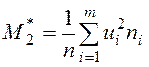 ,
,
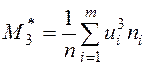 ,
, 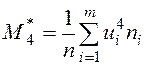 .
.
Числовые характеристики выборки вычисляем по формулам:
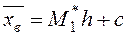 ;
; 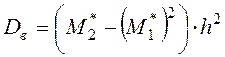 ;
; 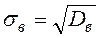 ;
;
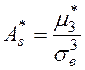 ;
; 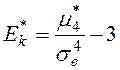 ,
,
где 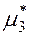 и
и 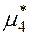 находим по формулам:
находим по формулам:
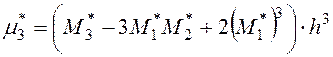 ,
,
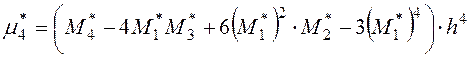 .
.
Пример 5. Вычислить числовые характеристики выборки, рассмотренной в примере 4 (табл.4), для которой построен интервальный ряд (табл.5).
¦ В качестве вариантов 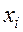 возьмем середины интервалов. Перейдем к условным вариантам.
возьмем середины интервалов. Перейдем к условным вариантам.
Вариант, значение которого 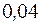 , имеет наибольшую частоту и находится в середине ряда. Примем его за «ложный ноль» (начало отсчета).
, имеет наибольшую частоту и находится в середине ряда. Примем его за «ложный ноль» (начало отсчета).
Условные варианты найдем по формуле:
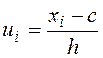 ,
,
где 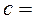
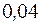 ,
, 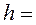
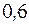 .
.
Составим расчетную табл.8 по форме табл.7
Таблица 8
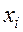 | 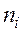 | 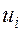 | 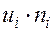 | 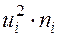 | 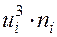 | 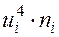 | 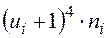 |
| -1,76 | -3 | -6 | -54 | ||||
| -1,16 | -2 | -12 | -48 | ||||
| -0,56 | -1 | -11 | -11 | ||||
| 0,04 | |||||||
| 0,64 | |||||||
| 1,24 | |||||||
| 1,84 | |||||||
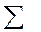 | -6 | -24 |
Контроль: 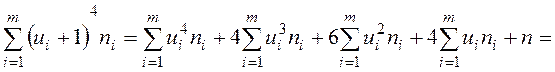
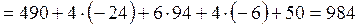 . Расчеты проведены верно.
. Расчеты проведены верно.
По данным табл. 8 находим условные моменты:
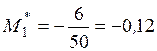 ,
, 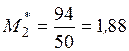 ,
,
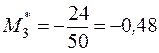 ,
, 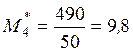 .
.
Находим числовые характеристики выборки:
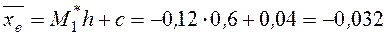
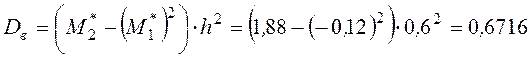
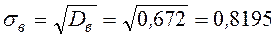
Вычислим центральные моменты третьего и четвертого порядка:
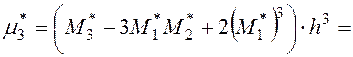
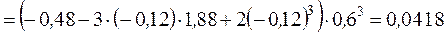
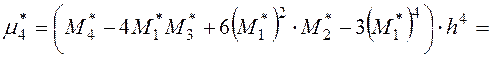
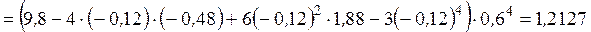
Вычислим выборочные коэффициенты асимметрии и эксцесса:
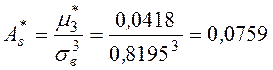
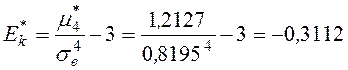 .?
.?
 2014-02-02
2014-02-02 2519
2519
