Статистическое распределение изображается графически с помощью полигона и гистограммы.
Определение. Полигоном частот называют ломаную, отрезки которой соединяют точки с координатами 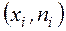 ; полигоном частостей – с координатами
; полигоном частостей – с координатами 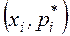 , где
, где 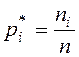 ,
, 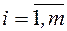 .
.
Полигон служит для изображения дискретного статистического ряда.
Полигон частостей является аналогом многоугольника распределения дискретной случайной величины в теории вероятностей.
Определение. Гистограммой частот (частостей) называют ступенчатую фигуру, состоящую из прямоугольников, основания которых расположены на оси 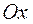 и длины их равны длинам частичных интервалов
и длины их равны длинам частичных интервалов 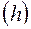 , а высоты равны отношению:
, а высоты равны отношению:
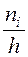 - для гистограммы частот;
- для гистограммы частот; 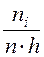 - для гистограммы частостей.
- для гистограммы частостей.
Гистограмма является графическим изображением интервального ряда.
Площадь гистограммы частот равна 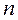 , а гистограммы частостей равна 1.
, а гистограммы частостей равна 1.
Можно построить полигон для интервального ряда, если его преобразовать в дискретный ряд. В этом случае интервалы заменяют их серединными значениями и ставят в соответствие интервальные частоты (частости). Полигон получим, соединив отрезками середины верхних оснований прямоугольников гистограммы.
Пример 3. Дана выборка значений случайной величины 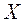 объема 20:
объема 20:
12, 14, 19, 15, 14, 18, 13, 16, 17, 12
18, 17, 15, 13, 17, 14, 14, 13, 14, 16
Требуется: - построить дискретный вариационный ряд;
- найти размах варьирования 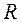 , моду
, моду 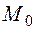 , медиану
, медиану 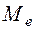 ;
;
- построить полигон частостей.
¦ 1)Ранжируем выборку: 12, 12, 13, 13, 13, 14, 14, 14, 14, 14,
15, 15, 16, 16, 17, 17, 17, 18, 18, 19.
2) Находим частоты вариантов и строим дискретный вариационный ряд (табл.3)
Таблица 3.
Значения вариантов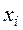 | |||||||||
Частоты 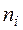 | 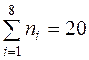 | ||||||||
Частости 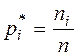 | 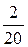 | 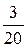 | 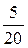 | 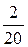 | 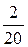 | 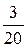 | 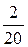 | 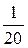 | 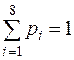 |
3) По результатам таблицы 3 находим:
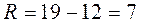 ,
, 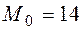 ,
, 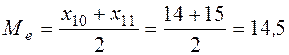
4)Строим полигон частостей.
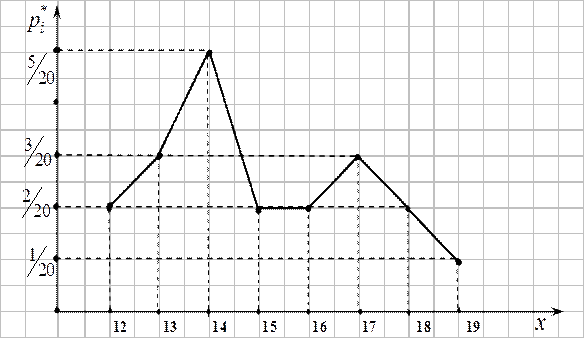
Рис. 2?
Пример 4. Результаты измерений отклонений от нормы диаметров
50 подшипников дали численные значения (в мкм), приведенные в табл. 4.
Таблица 4.
| -1,760 | -0,291 | -0,110 | -0,450 | 0,512 |
| -0,158 | 1,701 | 0,634 | 0,720 | 0,490 |
| 1,531 | -0,433 | 1,409 | 1,740 | -0,266 |
| -0,058 | 0,248 | -0,095 | -1,488 | -0,361 |
| 0,415 | -1,382 | 0,129 | -0,361 | -0,087 |
| -0,329 | 0,086 | 0,130 | -0,244 | -0,882 |
| 0,318 | -1,087 | 0,899 | 1,028 | -1,304 |
| 0,349 | -0,293 | 0,105 | -0,056 | 0,757 |
| -0,059 | -0,539 | -0,078 | 0,229 | 0,194 |
| 0,123 | 0,318 | 0,367 | -0,992 | 0,529 |
Для данной выборки: - построить интервальный вариационный ряд;
- построить гистограмму и полигон частостей.
¦ 1. Строим интервальный ряд.
По данным таблицы 4 определяем: 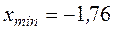 ;
; 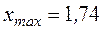
Для определения длины интервала 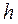 используем формулу Стерджеса:
используем формулу Стерджеса:
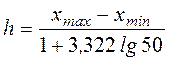 .
.
Число интервалов 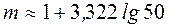 .
.
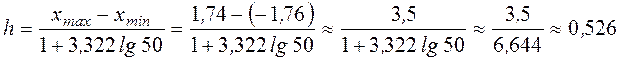
Примем 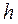 =0,6,
=0,6, 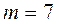 .
.
За начало первого интервала примем величину
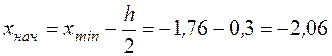 .
.
Конец последнего интервала должен удовлетворять условию:
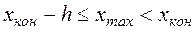 .
.
Действительно, 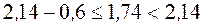 ;
; 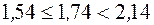 .
.
Строим интервальный ряд (табл. 5).
Таблица 5.
| Интервалы | 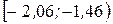 | 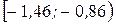 | 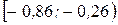 | 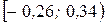 |
| Подсчет частот |  |  |  |  |
Частоты 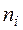 | ||||
Частости 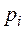 | 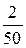 | 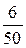 | 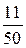 | 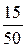 |
| Интервалы | 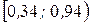 | 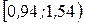 | 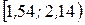 | |
| Подсчет частот |  |  |  | |
Частоты 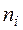 | 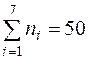 ; ; | |||
Частости 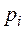 | 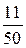 | 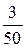 | 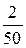 | 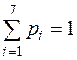 . . |
Строим гистограмму частостей.
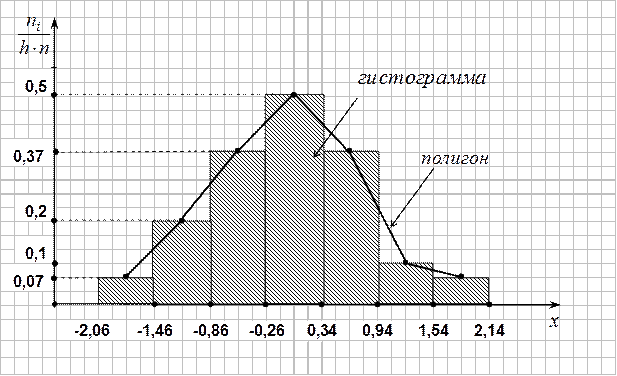
Рис.3
Вершинами полигона являются середины верхних оснований прямоугольников гистограммы.
Убедимся, что площадь гистограммы равна 1.
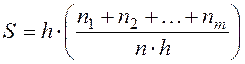
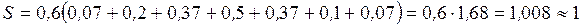 ?
?
 2014-02-02
2014-02-02 6434
6434








