Типовые динамические звенья
Типовыми динамическими звеньями называются звенья, описываемые дифференциальными уравнениями не выше второго порядка. Такие звенья классифицируются в зависимости от вида левой и правой частей их дифференциальных уравнений. Их можно разделить на три группы:
- позиционные;
- интегрирующие;
- дифференцирующие.
Каждая из этих групп, в свою очередь содержит несколько типовых звеньев.
Рассмотрим наиболее часто встречающиеся на практике типовые динамические звенья и определим для каждого из них основные характеристики:
- передаточную функцию;
- переходную функцию:
- импульсную переходную функцию (функцию веса);
- амплитудно-фазовую частотную характеристику;
- амплитудную частотную характеристику;
- фазовую частотную характеристику;
- логарифмические частотные характеристики (ЛАЧХ, ЛФЧХ).
1. Позиционные звенья – такие звенья, для которых в установившемся режиме характерна линейная зависимость между входной и выходной величинами.
Эти звенья описываются линейным диф. уравнением вида:
D(p)x(t)=b0g(t) (1)
где D(p) – многочлен не выше второго порядка.
При постоянном входном сигнале выходная величина устойчивых позиционных звеньев с течением времени стремится к постоянному значению.
а) Безинерционное (идеальное) усилительное звено.
Звено, как в установившемся, так и в переходном режиме описывается уравнением вида:
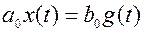 или
или 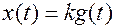 ,
,
где k – коэффициент передачи (усиления).
Передаточная функция звена 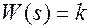 .
.
Переходная функция 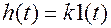 ;
;
Весовая функция 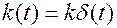
АФХ
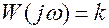
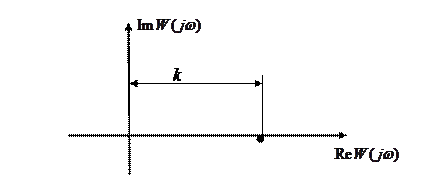
АЧХ 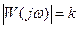
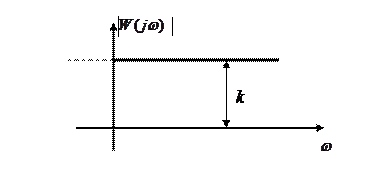
ФЧХ 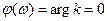

ЛАЧХ и ЛФЧХ 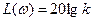
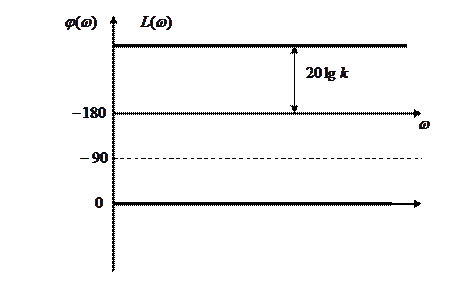
Любое устройство, описываемое дифференциальным уравнением вида
(a0p+ a1)x(t)=b0g(t)
Деля на a1, получим
(Tp+1)x(t)=kg(t),
где 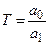 - постоянная времени звена,
- постоянная времени звена,
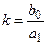 - коэффициент передачи звена.
- коэффициент передачи звена.
Передаточная функция звена
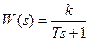 .
.
Определим переходную характеристику с помощью преобразования Лапласа. Т.к.
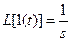 ,
,
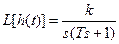 ,
,
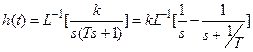 или
или
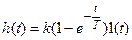 .
.

Теоретически переходной процесс длится бесконечно долго. Практически для этого звена под временем переходного процесса понимается наименьший промежуток времени, по истечении которого выполняется неравенство:
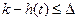 ,
,
где 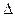 - наперед заданное положительное число
- наперед заданное положительное число
[обычно 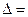 (0,01 – 0,05) k. ], или tп= (3 – 5)T.
(0,01 – 0,05) k. ], или tп= (3 – 5)T.
Учитывая, что
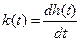 , найдем, что
, найдем, что
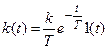 - функция веса.
- функция веса.

АФХ 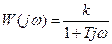 .
.
Построим АФХ в координатах Re и Im функции 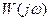 . Для этого представим
. Для этого представим 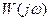 в виде:
в виде:
 .
.
Умножим числитель и знаменатель на сопряженный множитель
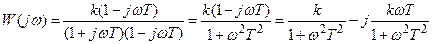 .
.
Обозначим
 ;
; 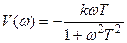 .
.
Исключим из них 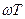 :
:
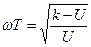 , подставив в
, подставив в 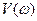 , получим:
, получим:
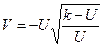 , или возводя в квадрат
, или возводя в квадрат
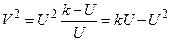 .
.
Добавляя и вычитая из правой части 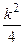 , получим
, получим
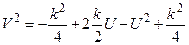 , или
, или
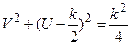 - окружность с центром, смещенным на
- окружность с центром, смещенным на 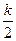 по действительной оси и радиусом
по действительной оси и радиусом 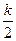 .
.


АЧХ 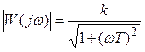
|

ФЧХ 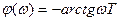
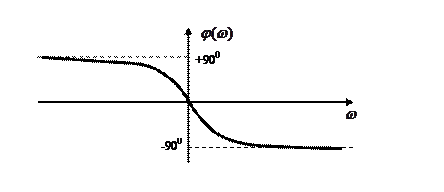
Логарифмическая частотная характеристика ЛАЧХ апериодического звена
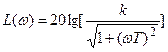 .
.
При  ,
, 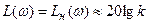
При  ,
, 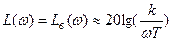 .
.
Характеристики 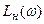 и
и 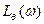 называют низкочастотной и высокочастотной асимптотами.
называют низкочастотной и высокочастотной асимптотами.
Заметим, что при 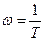
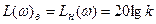 .
.
Частота, на которой сопрягаются эти характеристики, называется сопрягающей частотой.
Ломаная линия с уравнением
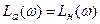 при
при 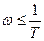 и
и
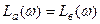 при
при 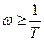 называется асимптотической ЛАЧХ апериодического звена.
называется асимптотической ЛАЧХ апериодического звена.
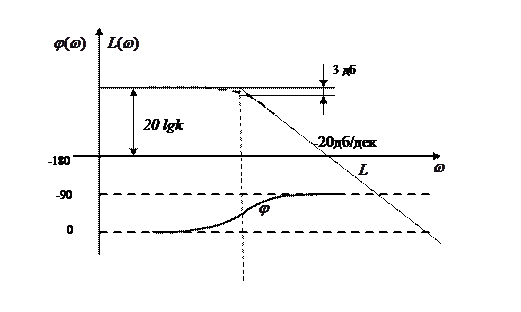
Если построить реальную ЛАЧХ по точкам, можно убедится, что максимальное отличие от асимптотической имеет место на сопрягающей частоте. Оно не велико (меньше 3 дб). Практически можно считать, что реальная и асимптотическая ЛАЧХ совпадают и ограничиваться построением асимптотических характеристик.
Фазовая логарифмическая характеристика ЛФЧХ
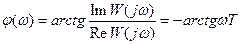
строится по точкам.
Звено любой физической природы (маятник, колебательный контур и т.д.), описываемое диф. уравнением вида:
(a0p2+ a1p+a2)x(t)=b0g(t)
при определенных соотношениях параметров a1 называется колебательным звеном. Разделив на a2, получим:
(Т2p2+2 Тp+1)x(t)=kg(t),
Тp+1)x(t)=kg(t),
где 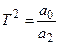 постоянная времени,
постоянная времени,
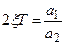 ;
;
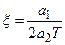 ;
;
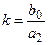 .
.
Передаточная функция колебательного звена
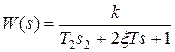 .
.
 =0
=0
имеет комплексные корни:
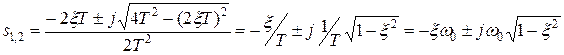 ,
,
где  .
.
Выражение для переходной функции найдем используя обратное преобразование Лапласа:
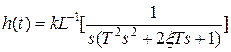 .
.
Разложив на простые дроби, в соответствии с таблицей оригиналов и изображений, получим
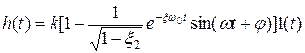 ,
,
где 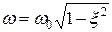 ;
;
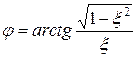 .
.
Продифференцировав полученное выражение, определим функцию веса:
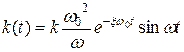 .
.
Переходной процесс рассматриваемого звена носит характер затухающих по экспоненте колебаний.
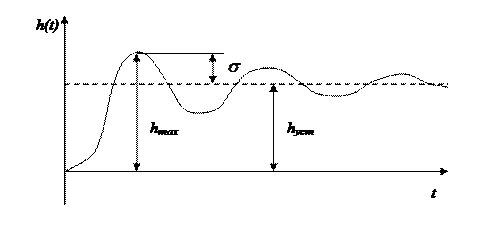
Практически важно определить время затухания переходного процесса tп – начальный промежуток времени, по истечении которого выполняется неравенство
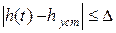 ,
,
где 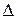 - наперед заданное положительное число. Более грубо можно считать, что процесс закончится тогда, когда затухли «сжимающие» его экспоненты.
- наперед заданное положительное число. Более грубо можно считать, что процесс закончится тогда, когда затухли «сжимающие» его экспоненты.
Иногда полезно знать максимальное отклонение 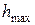 или величину перерегулирования
или величину перерегулирования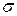 . Их можно вычислить по формуле
. Их можно вычислить по формуле
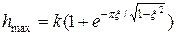 :
:
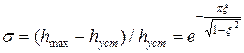 .
.
Как видно величина перерегулирования зависит только от относительного коэффициента затухания (коэффициента демпфирования) 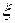 .
.
Амплитудно - фазовая характеристика, соответствующая передаточной функции будет
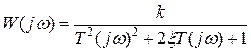 .
.
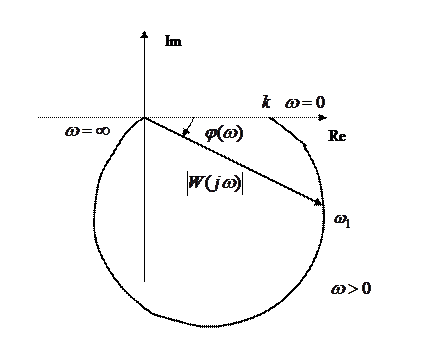
Имея такую характеристику, легко определить значения амплитуды и начальной фазы вынужденных колебаний х(t) на выходе системы при наличии на ее входе гармонического управляющего воздействия 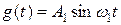 .
.
Амплитудно-частотная характеристика имеет вид:
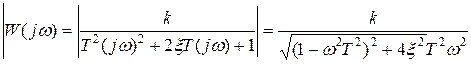 ,
,
а фазовая частотная характеристика
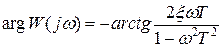 .
.
Найдем 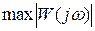 , для чего определим минимум подкоренного выражения в знаменателе и, приравняв его к нулю, получим
, для чего определим минимум подкоренного выражения в знаменателе и, приравняв его к нулю, получим
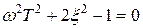 .
.
Следовательно, экстремум будет существовать на частоте
При 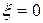 частота
частота 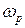 совпадает с собственной частотой
совпадает с собственной частотой 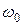 колебаний системы.
колебаний системы.
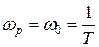 .
.
Подставив 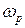 выражение для АЧХ, найдем ее максимальное значение
выражение для АЧХ, найдем ее максимальное значение
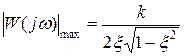 .
.
Чем меньше значение 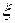 , тем больше
, тем больше  max. При
max. При ,
, 
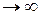 .
.


Выражение для логарифмической АЧХ имеет вид:
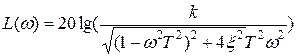 .
.
Асимптотическая ЛАЧХ будет состоять из двух участков:
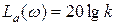 при
при 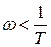 ;
;
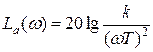 при
при 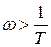 ;
;
|
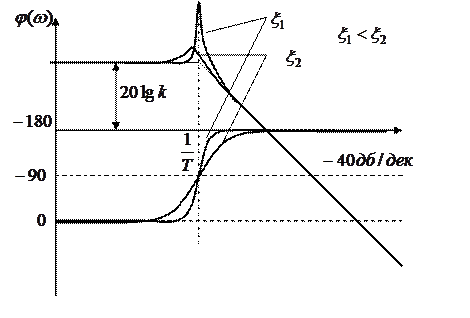
При 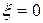 получаем консервативное звено с передаточной функцией
получаем консервативное звено с передаточной функцией
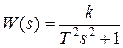 .
.
Все его характеристики могут быть получены из характеристик колебательного звена при 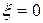 .
.
 2014-02-02
2014-02-02 1146
1146

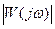
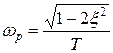 -
-