1. Вычисляем 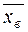 и
и 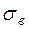 (см. Пример 5).
(см. Пример 5).
2. Находим теоретические частоты 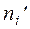 .
.
Их можно вычислить двумя способами.
Первый способ
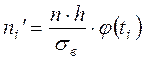 ,
,
где 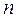 - объем выборки,
- объем выборки, 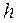 - шаг,
- шаг, 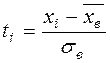 ;
;
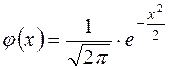 - функция Гаусса, значение которой в точке
- функция Гаусса, значение которой в точке 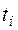
находим по таблице (Приложение 1).
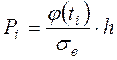 - вероятность попадания значений случайной
- вероятность попадания значений случайной
величины 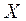 в
в 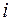 - й интервал.
- й интервал.
Для вычисления 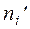 составляем табл. 9.
составляем табл. 9.
Таблица 9
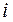 | 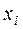 | 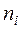 | 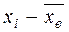 | 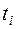 | 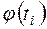 | 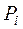 | 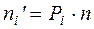 |
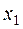 | 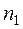 | 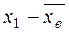 | 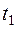 | 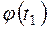 | 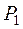 | 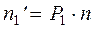 | |
 |  |  |  |  |  |  |  |
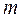 | 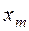 | 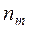 | 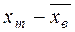 | 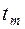 | 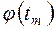 | 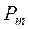 | 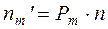 |
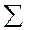 | 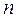 | 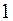 | 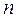 |
Второй способ.
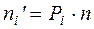
где 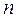 - объем выборки,
- объем выборки, 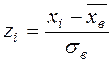 ,
,
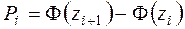 - вероятность попадания
- вероятность попадания 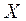 в
в 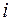 - й интервал,
- й интервал,
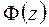 - значение функции Лапласа (Приложение 2).
- значение функции Лапласа (Приложение 2).
Полагают 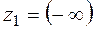 ,
, 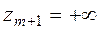 .
.
Для вычисления 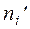 составляем табл. 10.
составляем табл. 10.
Таблица 10
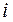 | Границы интервала | 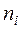 | Границы интервала | 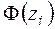 | 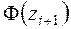 | 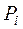 | 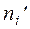 | ||
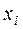 | 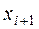 | 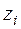 | 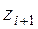 | ||||||
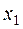 | 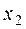 | 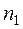 | 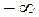 | 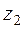 | -0,5 | 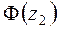 | 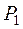 | 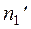 | |
 |  |  |  |  |  |  |  |  |  |
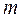 | 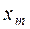 | 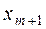 | 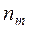 | 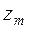 | 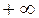 | 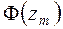 | 0,5 | 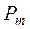 | 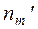 |
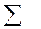 | 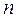 | 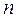 |
3. Сравниваем эмпирические (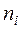 ) и теоретические (
) и теоретические (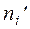 ) частоты с помощью критерия Пирсона.
) частоты с помощью критерия Пирсона.
Для этого:
1) составляем расчетную табл.11, по которой находим
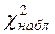 - наблюдаемое значение критерия
- наблюдаемое значение критерия 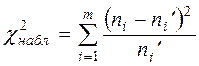
Таблица 11.
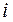 | 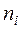 | 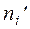 | 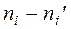 | 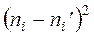 | 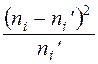  | 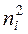 | 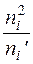 |
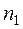 | 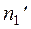 | 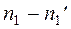 | 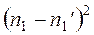 | 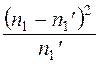 | 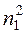 | 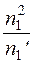 | |
 |  |  |  |  |  |  |  |
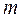 | 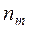 | 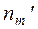 | 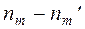 | 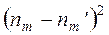 | 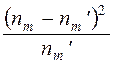 | 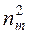 | 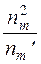 |
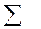 | 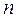 | 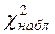 |
Контроль: 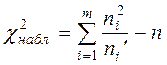 .
.
2) Находим число степеней свободы 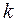 :
: 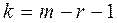
где 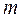 - число интервалов;
- число интервалов; 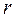 - число параметров предполагаемого распределения,
- число параметров предполагаемого распределения,
Для нормального распределения 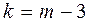 , так как
, так как 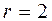 (нормальный закон распределения характеризуется двумя параметрами
(нормальный закон распределения характеризуется двумя параметрами 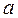 и
и 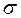 ).
).
4. В таблице критических точек (квантилей) распределения 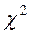
(Приложение 3) по заданному уровню значимости 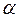 и числу степеней свободы
и числу степеней свободы
находим 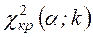 правосторонней критической области.
правосторонней критической области.
Если 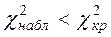 - нет оснований отвергнуть гипотезу
- нет оснований отвергнуть гипотезу 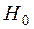
о нормальном распределении генеральной совокупности.
Если 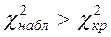 - гипотезу отвергаем.
- гипотезу отвергаем.
Замечание.
1) Объем выборки должен быть достаточно велик 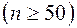 .
.
2) Малочисленные частоты 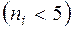 следует объединить. В этом случае и соответствующие им теоретические частоты также надо сложить.
следует объединить. В этом случае и соответствующие им теоретические частоты также надо сложить.
Если производилось объединение частот, то при определении числа степеней свободы по формуле 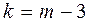 следует в качестве
следует в качестве 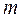 принять число интервалов, оставшихся после объединения частот.
принять число интервалов, оставшихся после объединения частот.
Пример 10. Пусть из генеральной совокупности 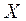 задана выборка объемом 50 (табл.4). Требуется проверить гипотезу
задана выборка объемом 50 (табл.4). Требуется проверить гипотезу 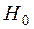 о нормальном распределении генеральной совокупности по данной выборке.
о нормальном распределении генеральной совокупности по данной выборке.
¦ 1. Из рассмотренных выше примеров известно:
- интервальный ряд табл. 12
Таблица 12
| Интервалы | 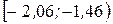 | 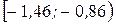 | 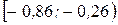 | 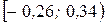 |
Частоты 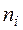 |
| Интервалы | 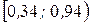 | 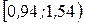 | 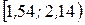 | |
Частоты 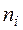 | 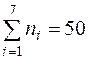 . . |
- числовые характеристики выборки 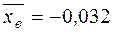 ,
, 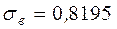 ,
,
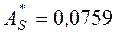 ,
, 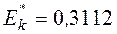 (см. Пример 5).
(см. Пример 5).
2. Проверим гипотезу 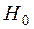 с помощью средних квадратических отклонений коэффициентов
с помощью средних квадратических отклонений коэффициентов 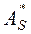 и
и 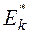 .
.
Критерием распределения выборки по нормальному закону является равенство нулю коэффициентов 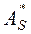 и
и 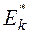 .
.
Если они отличны от нуля, то для предварительного выбора закона распределения вычисляют средние квадратические отклонения для 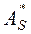 и
и 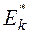 :
:
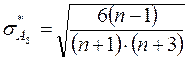
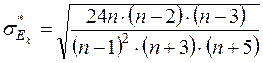
Если 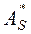 и
и 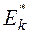 отличаются по модулю от нуля не более чем на удвоенные средние квадратические отклонения, то есть
отличаются по модулю от нуля не более чем на удвоенные средние квадратические отклонения, то есть 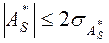 и
и 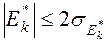 , то можно предположить, что данная выборка распределена по нормальному закону.
, то можно предположить, что данная выборка распределена по нормальному закону.
Рассчитаем 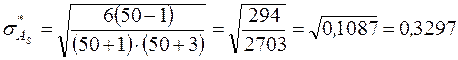
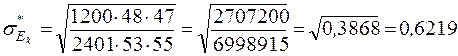 .
.
Для 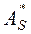 условие критерия выполняется:
условие критерия выполняется: 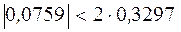 .
.
Для 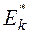 условие критерия выполняется:
условие критерия выполняется: 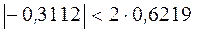 .
.
Гипотезу 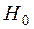 принимаем, то есть можно предположить, что генеральная совокупность
принимаем, то есть можно предположить, что генеральная совокупность 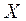 распределена по нормальному закону.
распределена по нормальному закону.
3. Проверим гипотезу 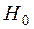 по критерию Пирсона.
по критерию Пирсона.
1) 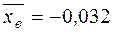 ,
, 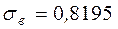 .
.
2) Найдем теоретические частоты 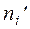 вторым способом.
вторым способом.
Интервальный ряд (табл.12) содержит интервалы с частотами меньшими 5. Следовательно, два первых и два последних интервала объединяем, при этом соответствующие частоты суммируем.
Составим расчетную табл.13 по форме табл.10.
Таблица 13
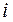 | Границы интервала | 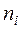 | Границы интервала | 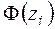 | 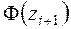 | 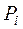 | 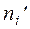 | ||
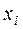 | 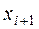 | 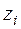 | 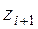 | ||||||
| -2,06 | -0,86 | 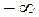 | -1,01 | -0,5 | -0,3438 | 0,1562 | 7,81 | ||
| -0,86 | -0,26 | -1,01 | -0,28 | -0,3438 | -0,1103 | 0,2335 | 11,675 | ||
| -0,26 | 0,34 | -0,28 | 0,45 | -0,1103 | 0,1736 | 0,2839 | 14,195 | ||
| 0,34 | 0,94 | 0,45 | 1,19 | 0,1736 | 0,3830 | 0,2094 | 10,47 | ||
| 0,94 | 2,14 | 1,19 | 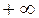 | 0,3830 | 0,5 | 0,1170 | 5,85 | ||
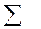 |
3) Сравним эмпирические (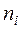 ) и теоретические (
) и теоретические (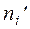 ) частоты. Для этого составляем расчетную табл.14 по форме табл.11
) частоты. Для этого составляем расчетную табл.14 по форме табл.11
Таблица 14
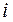 | 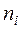 | 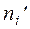 | 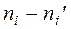 | 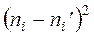 | 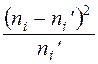  | 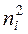 | 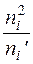 |
| 7,810 | 0,190 | 0,0361 | 0,0046 | 8,1946 | |||
| 11,675 | -0,675 | 0,4556 | 0,0390 | 10,3640 | |||
| 14,195 | 0,805 | 0,6480 | 0,0457 | 15,8507 | |||
| 10,470 | 0,530 | 0,2809 | 0,0268 | 11,5568 | |||
| 5,850 | -0,850 | 0,7225 | 0,1235 | 4,2735 | |||
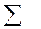 | 0,2396 | 50,2396 |
Контроль: 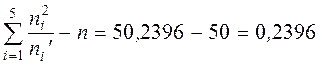
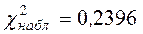 . Расчеты проведены верно.
. Расчеты проведены верно.
4) Зададим 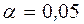 .
.
Вычислим число степеней свободы 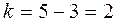 и найдем
и найдем 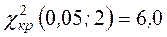 (Приложение 3). Получим
(Приложение 3). Получим 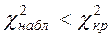 .
.
Следовательно, нет оснований отвергать гипотезу 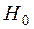 о нормальном распределении генеральной совокупности
о нормальном распределении генеральной совокупности 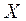 .
.
Другими словами различие между эмпирическими (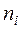 ) и теоретическими (
) и теоретическими (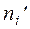 ) частотами незначительное (случайное), которое можно объяснить малым объемом выборки.
) частотами незначительное (случайное), которое можно объяснить малым объемом выборки.
Построим нормальную кривую. Для этого составим табл.15.
Таблица 15
| Середины интервалов | -1,76 | -1,16 | -0,56 | 0,04 | 0,64 | 1,24 | 1,84 |
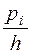 | 0,05 | 0,19 | 0,39 | 0,52 | 0,34 | 0,14 | 0,03 |
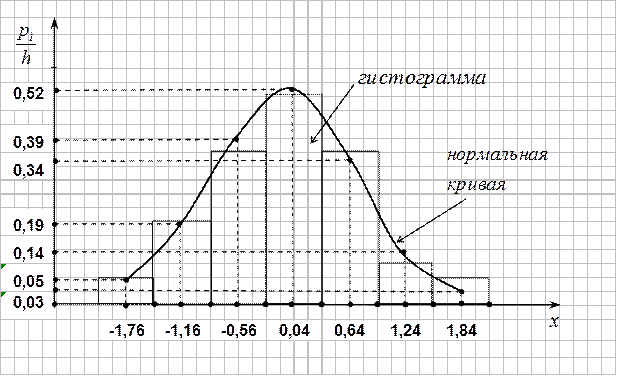
Рис.5
Так как гипотеза о нормальном распределении не отвергается, то нормальная кривая хорошо сглаживает гистограмму.?
 2014-02-02
2014-02-02 816
816








