2014-02-02
1001
Отыскание параметров выборочного уравнения линейной регрессии
Пусть имеются две случайные величины, и проводится их измерение.
В результате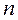 
независимых опытов получены, 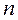пар чисел 
, 
, 
, 
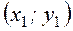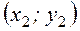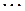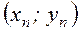
Будем искать линейное выборочное уравнение регрессии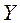 
на 
в виде:
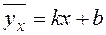
Так как по выборочным данным можно получить только оценки параметров, то оценку коэффициента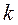 
обозначим через 
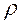, а оценку 
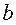— через 
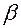, то есть 
.
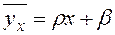Параметры 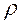и 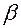находим методом наименьших квадратов по формулам:
,
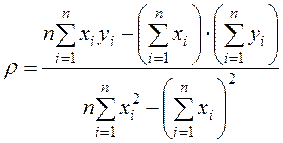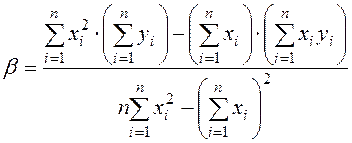
Аналогично находится выборочное уравнение линейной регрессии на :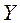
,
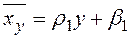где
,
.
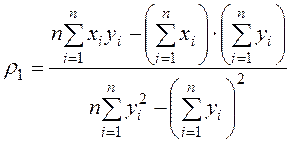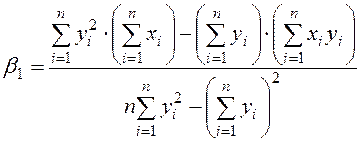Для оценки связи (тесноты) между случайными величинами обычно используется выборочная ковариация и выборочный коэффициент корреляции.
Выборочная ковариация (эмпирический корреляционный момент) записывается в виде:
,
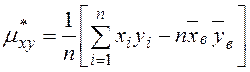а выборочный коэффициент корреляции имеет вид:
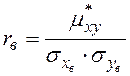или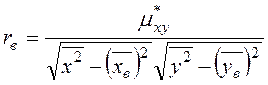 
,
где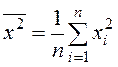 
, 
.
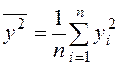Абсолютная величина (модуль) выборочного коэффициента корреляции не превосходит единицы, то есть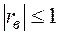 
или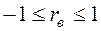 
. С возрастанием 
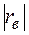линейная корреляционная зависимость становится более тесной, и при 
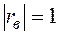переходит в функциональную. Если 
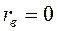, то корреляционная связь испытаний и отсутствует.
|
|
|
Пример 11. В результате независимых испытаний получены пары значений случайных величин и :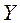
| |||||
|
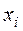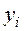В таблице значения расставлены в возрастающем порядке.
Найти выборочное уравнение линейной регрессии и выборочный коэффициент корреляции. Построить прямые регрессии 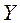на и на .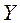
¦ Составим таблицу подсчетов (табл.16).
Таблица 16
Номер опыта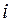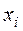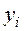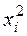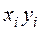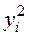 
|
|
| 
| 
| 
|
|
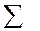1) Находим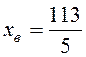 
, 
.
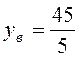2) 
, 
.
, 
.
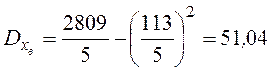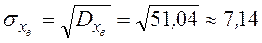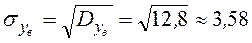3) Вычислим эмпирический корреляционный момент:
.
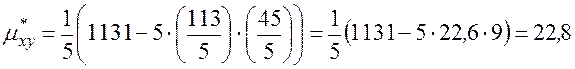Тогда коэффициент корреляции: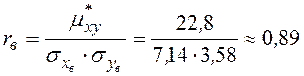 
.
Значение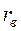 
довольно близко к 1, следовательно, связь между случайными величинами и 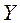довольно тесная.
4) Найдем уравнения линий регрессии
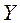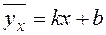
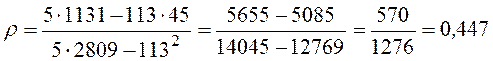
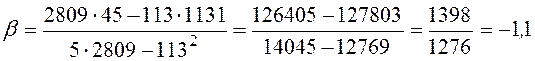
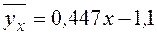
на :
на :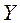
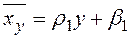
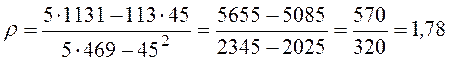
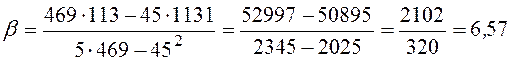
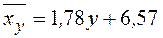
5) Построим линии регрессии (Рис.6). Для этого найдем точки пересечения линий с осями координат:
: 
, 
;
, 
: 
, 
;
, 
.
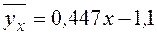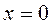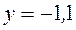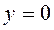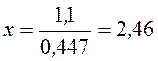
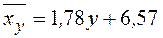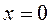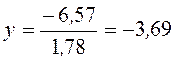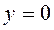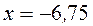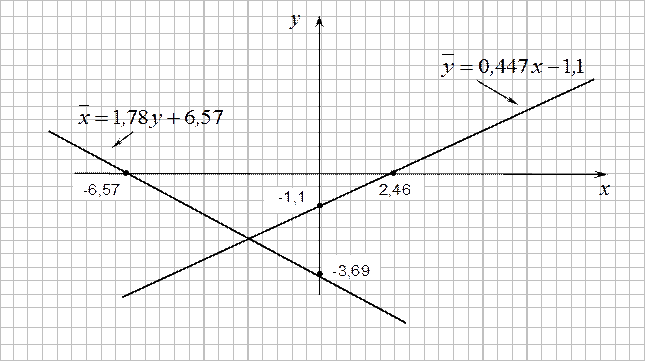
Рис.6?
