Опр. Коммутатором двух операторов 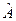 и
и 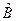 называется оператор
называется оператор 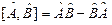 .
.
Произведение операторов 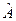 и
и 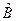 ,вообще говоря, не коммутативно, т.е.
,вообще говоря, не коммутативно, т.е. 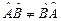 .
.
Опр. Операторы, для которых выполняется условие 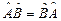 называются коммутирующими.
называются коммутирующими.
Пример 1. Вычислим 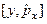 . Для этого рассмотрим действие коммутатора на произвольную функцию Y.
. Для этого рассмотрим действие коммутатора на произвольную функцию Y. 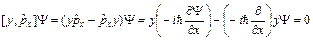 , т.е.
, т.е. 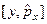 =0, эти операторы коммутируют между собой.
=0, эти операторы коммутируют между собой.
Пример 2. Вычислим 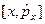 .
. 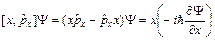
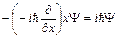 ,т.е.
,т.е. 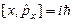 , операторы не коммутируют между собой.
, операторы не коммутируют между собой.
Пусть некоторое состояние квантовой системы описывается волновой функцией Y. Произведем в этом квантовом состояние измерение двух физических величин А и В. Этим величинам соответствуют операторы 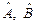 . Физические величины могут быль одновременно измерены, если функция Y является собственной функцией обоих операторов, т. е. выполняются условия:
. Физические величины могут быль одновременно измерены, если функция Y является собственной функцией обоих операторов, т. е. выполняются условия:
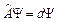 (1)
(1)
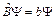 (2)
(2)
Подействуем на обе части равенства (1) оператором 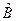 , а на (2) – оператором
, а на (2) – оператором 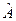 :
:
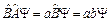 , (3)
, (3)
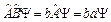 . (4)
. (4)
Из (3) и (4) следует, что 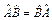 . Т.е. если две физические величины одновременно измеримы, то их операторы коммутируют. Верно и обратное утверждение: если два оператора
. Т.е. если две физические величины одновременно измеримы, то их операторы коммутируют. Верно и обратное утверждение: если два оператора 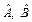 коммутируют, то физические величины А и В одновременно измеримы. Как видно из примеров 1 и 2, координата у и компонента импульса рх могут быть одновременно точно измеримы, а координата х и компонента импульса рх одновременно точно не могут быть измерены.
коммутируют, то физические величины А и В одновременно измеримы. Как видно из примеров 1 и 2, координата у и компонента импульса рх могут быть одновременно точно измеримы, а координата х и компонента импульса рх одновременно точно не могут быть измерены.
|
|
|
Свойство коммутативности не является транзитивным. Если 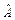 коммутирует с
коммутирует с 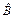 и
и 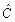 , то это не значит, что
, то это не значит, что 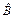 и
и 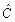 коммутируют между собой.
коммутируют между собой.
В квантовой механике используется понятие полного набора физических величин, которые для данной системы могут иметь одновременно определенные значения. Например, для свободно движущейся частицы – это импульс и энергия. Очевидно, что полный набор не может включать в себя импульсы и координаты частиц, так как они одновременно не имеют определенного значения. Для задания состояния квантовой системы достаточно задать только координаты частицы или только импульсы, или вообще любую совокупность величин, которые одновременно измеряются. Число таких величин должно быть равно числу степеней свободы системы.
Задание полного набора однозначно определяет волновую функцию системы. Полные наборы для разных состояний различны. В частном случае полный набор может состоять только из одной переменной. В таком состоянии все переменные, кроме одной, образующей полный набор, будут неопределенными. В качестве полного набора, однозначно определяющего волновую функцию системы, используют также квантовые числа, которые сохраняются в процессе движения. Например, состояние электрона в атоме определяется четырьмя квантовыми числами, соответствующим четырем степеням свободы электрона. Эти 4 степени свободы связаны с тремя пространственными координатами и спином. Для водородоподобных атомов 4 квантовых числа, образующих полный набор: n – главное квантовое число, l – орбитальное квантовое число, m – магнитное квантовое число, sz – спиновое.
|
|
|
13. Уравнение Шрёдингера. Принцип причинности. Стационарные состояния.
Уравнение Шрёдингера связано с гипотезой де Бройля. Согласно гипотезе де Бройля свободной частице с энергией Е и импульсом р, движущейся вдоль оси х, соответствует плоская волна
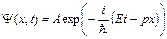 (1)
(1)
Продифференцируем (1) по времени:
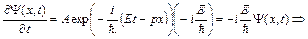
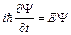 (2)
(2)
Продифференцируем (1) дважды по координате х: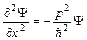 и учтем, что свободная частица обладает энергией
и учтем, что свободная частица обладает энергией 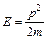 , тогда с учетом (2):
, тогда с учетом (2):
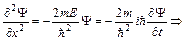
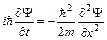 (3)
(3)
В общем случае свободного движения частицы в пространстве:
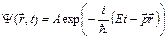 , уравнение (3) будет иметь вид:
, уравнение (3) будет иметь вид:
 или
или 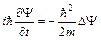 , (4)
, (4)
где 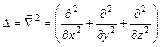 . Далее Шрёдингер предположил, что если частица движется в потенциальном поле
. Далее Шрёдингер предположил, что если частица движется в потенциальном поле 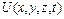 , то уравнение (4) должно быть видоизменено следующим образом:
, то уравнение (4) должно быть видоизменено следующим образом:
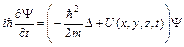 (5)
(5)
Уравнение (5) можно назвать уравнением движения квантовой частицы, оно является основным уравнением нерелятивистской квантовой механики. В квантовой механике уравнение Шрёдингера играет такую же роль, что и уравнение Ньютона в классической механике. Задать закон движения частицы в квантовой механике это значит определить значение волновой функции Y в любой момент времени t.
Для нахождения единственного значения функции Y кроме уравнения (5) необходимо определить начальные условия. Начальные условия определяют значение волновой функции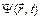 при t = 0. Кроме этого, волновая функция должна удовлетворять условию нормировки
при t = 0. Кроме этого, волновая функция должна удовлетворять условию нормировки 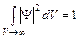 .
.
В квантовой механике поведение микрочастиц определяется закономерностями статистического типа и принцип причинности для микрочастиц формулируется следующим образом.
Пусть известно состояние частицы в начальный момент времени t = 0, то есть известно значение функции состояния 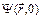 . Тогда решая уравнение Шрёдингера (5) можно однозначно определить её волновую функцию в последующие моменты времени
. Тогда решая уравнение Шрёдингера (5) можно однозначно определить её волновую функцию в последующие моменты времени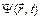 .
.
Из смысла волновой функции вытекает, что можно предсказать вероятности того, что характеризующие частицу физические величины будут иметь то или иное значение в любой момент времени t >0. Сформулированный таким образом принцип причинности в квантовой механике имеет более общий характер, чем лапласовский детерминизм в классической механике.
Если отсутствуют переменные внешние поля, действующие на частицу, т.е. 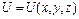 , то U имеет смысл потенциальной энергии и гамильтониан совпадает с оператором полной энергии. В этом случае волновую функцию можно представить в виде произведения двух функций, одна из которых зависит только от координат, другая – только от времени:
, то U имеет смысл потенциальной энергии и гамильтониан совпадает с оператором полной энергии. В этом случае волновую функцию можно представить в виде произведения двух функций, одна из которых зависит только от координат, другая – только от времени:
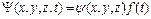 (6)
(6)
Подставив (6) в (5), получим 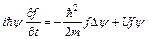 , разделим это уравнение на fy:
, разделим это уравнение на fy:
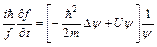 (7)
(7)
Левая часть уравнения (7) зависит только от времени, правая – только от координат. Это возможно только в том случае, когда обе части уравнения равны одной и той же постоянной величине.
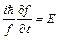 , (8)
, (8)
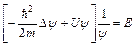 или
или 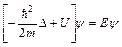 (9)
(9)
(9) называют стационарным уравнением Шрёдингера. Решение уравнения (8) имеет вид:
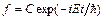 . (10)
. (10)
Тогда общее решение уравнения (5) в соответствии с представлением (6) будет иметь вид:
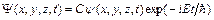 . (11)
. (11)
Отсюда следует, что плотность вероятности обнаружения частицы в различных точках пространства равна 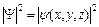 , т. е. не зависит от времени. Поэтому состояния, которые описываются функциями вида (11) называются стационарными состояниями.
, т. е. не зависит от времени. Поэтому состояния, которые описываются функциями вида (11) называются стационарными состояниями.
 2014-02-02
2014-02-02 10173
10173
