Возможные значения наблюдаемых и их вероятность. Средние значения наблюдаемых. Квантовомеханический принцип суперпозиции

В основе квантовой механики лежат несколько постулатов, которые были сформулированы в работах М. Борна, П. Дирака и др.

Один из постулатов утверждает, что квантовому состоянию системы можно сопоставить некоторую Ψ-функцию, которая полностью определяет данное состояние.

В соответствии со следующим постулатом квантовой механики каждой физической величине Q сопоставляется линейный оператор .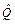

Любой оператор удовлетворяет уравнению

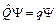. (1)

Значения параметра q, отвечающие уравнению (1) называются собственными значениями оператора 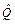. Функции, удовлетворяющие уравнению (1), называются собственными функциями оператора .

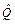В случае дискретного спектра собственные значения и собственные функции оператора 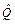можно пронумеровать: q ₁, q ₂, q ₃, … q _k, Ψ ₁, Ψ ₂, Ψ ₃, … Ψ _k. Тогда уравнению (1) отвечает набор уравнений

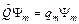, m= 1,…k. (2)

В квантовой механике предполагается, что совокупность собственных функций Ψ_m образует полный набор, т.е. любую непрерывную функцию Ψ можно представить в виде

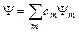(3)

В соответствии с остальными постулатами квантовой механики в результате измерения физической величины Q может получиться лишь одно из собственных значений q _m оператора 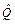, удовлетворяющих уравнению (2) и вероятность обнаружить значение q _m равна .

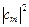Для коэффициентов с _m должно выполняться условие нормировки

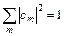и эти коэффициенты определяются как скалярное произведение функций Y_m и Y: 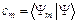(4),

причем 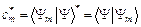(5)

Найдем среднее значение наблюдаемой величины, то есть математическое ожидание результатов измерений, используя постулаты квантовой механики и соотношения (4), (5), (2):

=

.

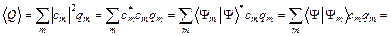
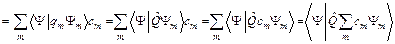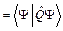Итак, мы получили формулу для расчета среднего значения физической величины Q в квантовом состоянии системы, описываемом волновой функцией Ψ:

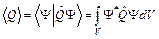(6)

Сформулируем одно из важных свойств квантовых состояний, которое называется квантово-механическим принципом суперпозиции: если частица может находиться в квантовых состояниях, которые описываются волновыми функциями Ψ₁, Ψ₂,…, Y_N то эта частица может также находиться в состоянии, описываемом волновой функцией

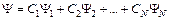(7)

где С ₁ и С ₂, C_N в общем случае комплексные числа.

Функции Ψ₁, Ψ₂,…Y_N являются функциями чистых состояний, Ψ – волновая функция смешанного состояния.

Отметим, что если в состоянии Ψ₁ частица, например, имела импульс р ₁, а в состоянии Ψ₂ – импульс р ₂, …, в состоянии Ψ_N – импульс р _N, то в смешанном состоянии Y при измерении импульса мы получим либо значение р ₁ либо р ₂, …, либо p _N.

Возможность состояний, в которых данная физическая величина не имеет определенного значения, и которые получаются суперпозицией состояний, с определенным значением этой величины, является характерной чертой квантовой механики, принципиально отличающей ее от классической механики. Описать такое "смешанное" состояние одной частицы на языке классической механики невозможно. Это свойство смешанных состояний сейчас используют в современных технологиях, разрабатывающих квантовые компьютеры, так как возможно использование логического элемента не только с двумя состояниями "0" и "1", но и элементов, которые могут находиться в состояниях суперпозиции нуля и единицы с некоторыми вероятностями. Такие элементы изменяют принцип работы компьютера и позволяют создавать алгоритмы, значительно повышающие быстродействие и эффективность переработки информации.