- Поступательное движение (рис. 7.1)
Скорости всех точек тела одинаковы по величине и направлению, также, как и ускорения.
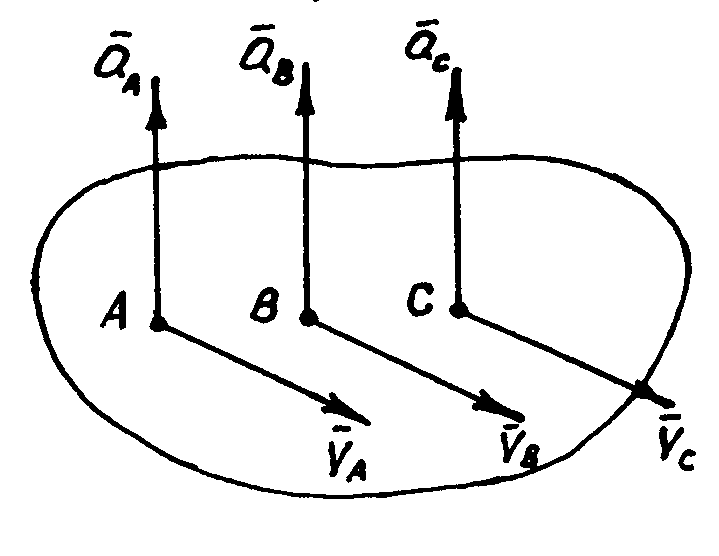 VА= VВ = Vс=
VА= VВ = Vс=
aА = aВ = аС =...
Рисунок 7.1
- Вращательное движение вокруг неподвижной оси (рис. 7.2)
LОА=│ОА│ 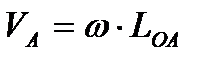
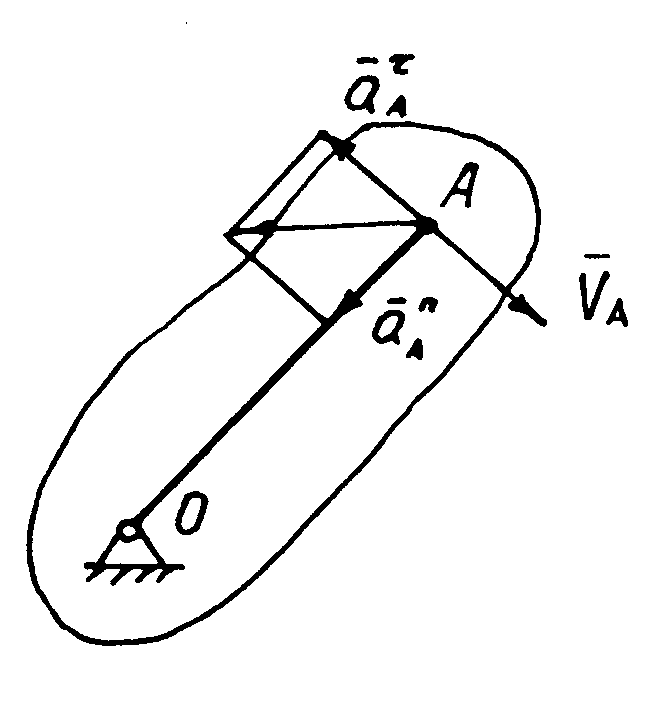 Рисунок 7.2 Рисунок 7.2 |
Векторскорости VА┴ОА и направлен в сторонудвижения, 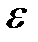 направлен против движения.
направлен против движения.
Ускорение разлагается на нормальное и касательное:
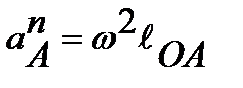 ;
; 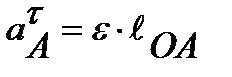 ;
; 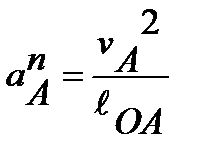 (7.1)
(7.1)
вектор 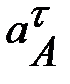 направлен так же, как и угловое ускорение
направлен так же, как и угловое ускорение 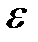 .
.
Если направления углового ускорения 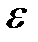 и угловой скорости
и угловой скорости 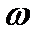 совпадают, то движение будет ускоренным.
совпадают, то движение будет ускоренным.
Если направления углового ускорения 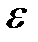 и угловой скорости
и угловой скорости 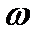 противоположены по направлению, то движение будет замедленное.
противоположены по направлению, то движение будет замедленное.
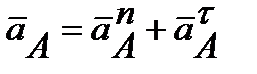 (7.2)
(7.2)
векторное уравнение.
По величине полное ускорение точки А будет равно:
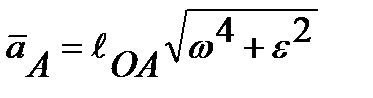 (7.3)
(7.3)
Угол отклонения вектора ускорения точки от радиуса можно определить по формуле:
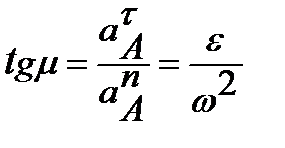 (7.4)
(7.4)
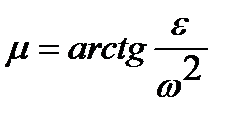 (7.5)
(7.5)
3.Плоскопараллельное движение (рис. 7.3)
Из теоретической механики известно, что движение какой-либо точки звена можно представить как сумму двух движений: из движения какой-либо другой точки А и движения самой точки В вокруг А.
т.е. 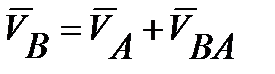 (7.6)
(7.6)
где
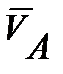 - вектор скорости точки А;
- вектор скорости точки А;
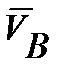 - вектор скорости точки В;
- вектор скорости точки В;
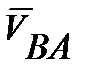 - вектор скорости точки В в движении вокруг точки А;
- вектор скорости точки В в движении вокруг точки А;
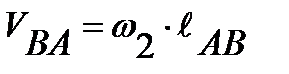 =>
=> 
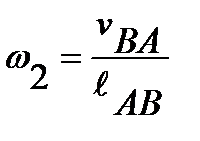

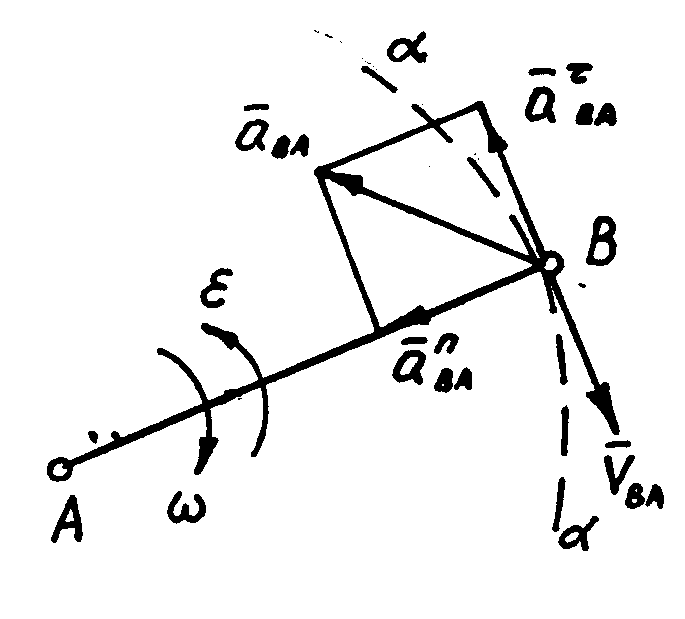 Рисунок 7.3 Рисунок 7.3 | Ускорение точки В также состоит из двух ускорений: где 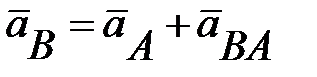 (*) (*) 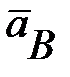 -вектор ускорения точки В -вектор ускорения точки В 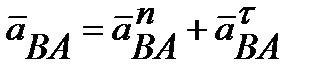 (7.7) (7.7) 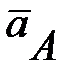 - вектор ускорения точки А; - вектор ускорения точки А; 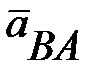 - вектор ускорения точки В вокруг точки А; - вектор ускорения точки В вокруг точки А; |
Уравнение (*) примет следующий вид:
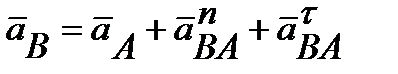 (7.8)
(7.8)
Направление векторов: 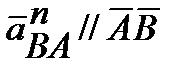 ,
, 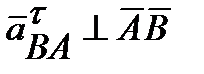
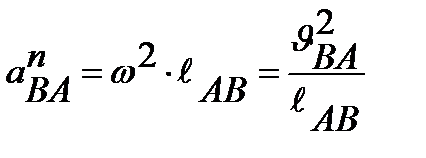 (7.9)
(7.9)
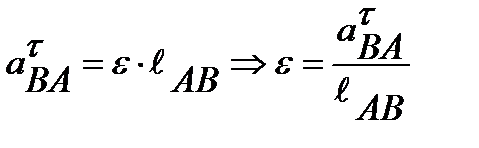 (7.10)
(7.10)
4. Две точки принадлежат двум звеньям, соединенным в поступательную кинематическую пару и в данный момент совпадают (рис. 7.4)
Точка А принадлежат звену 1, В – звену 2. В данный момент точка В находится над точкой А. Звенья 1 и 2 соединены в одну поступательную пару. Движение точки В состоит из двух движений: движения точки В вместе с точкой А и движения точки В относительно точки А.
Ускорение складывается из трех ускорении: ускорения точки А, ускорения относительно точки А и поворотного ускорения. В данном случае движение поступательное, поэтому относительное движение раскладывается только на касательное ускорение. Векторное уравнение имеет вид:
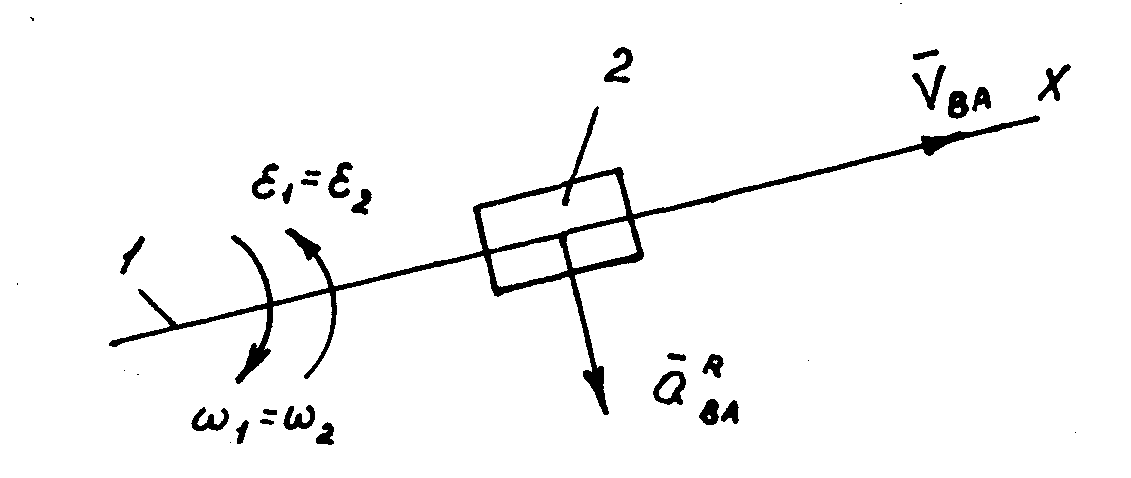
Рисунок 7.4
Поступательная кинематическая пара
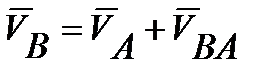 (7.11)
(7.11)
где V ВА // XX
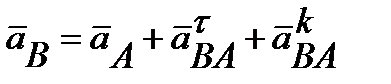 (7.12)
(7.12)
где 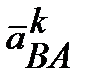 - поворотное ускорение точки В, относительно точки А;
- поворотное ускорение точки В, относительно точки А;
направление касательного вектора 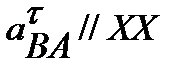 ;
;
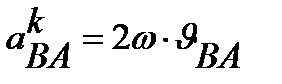 - кориолисово ускорение;
- кориолисово ускорение;
Направление вектора кориолисова ускорения 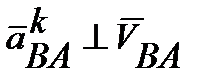 (по направлению
(по направлению 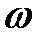 - угловая скорость)
- угловая скорость)
Определить скорости можно также и графическим способом при помощи так называемых планов скоростей. Планы скоростей строятся по векторным уравнениям, которые составляются отдельно для каждой групп Ассура.
Рассмотрим пример: Возьмем шарнирный четырехзвенник. Известны размеры звеньев lОА, lАВ, lВС, lОС, положение механизма, закон движения ведущего звена ω1=const.
Движение ведущего звена считаем равномерным.
Построение планов скоростей проводится в порядке построения механизма.
Скорость ведущего звена: VА=ω1 lОА - величина скорости точки А.
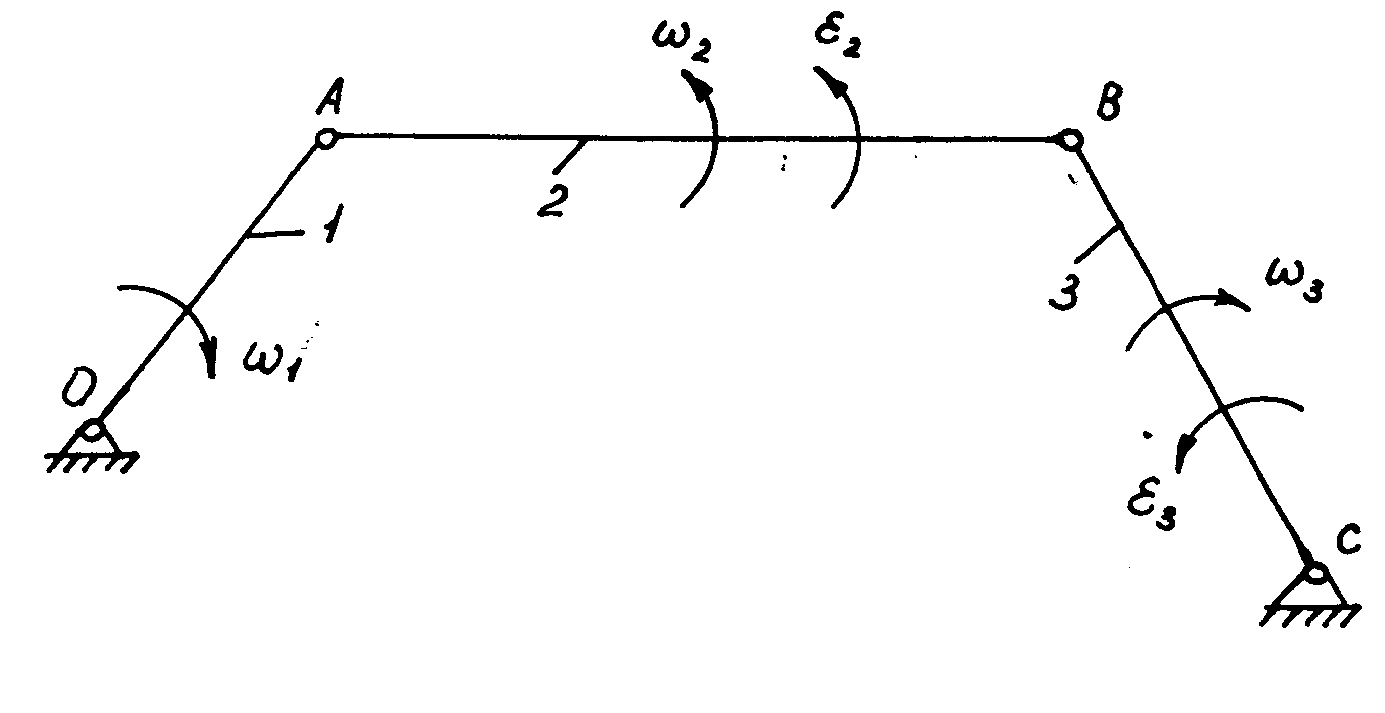
Рисунок 7.5
Направления угловых скоростей и угловых ускорений
плоского четырехзвенника.
Вектор скорости 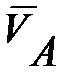 направлен ┴ звену ОА, в сторону направления угловой скорости ω 1. Скорость точки В определяется двумя способами:
направлен ┴ звену ОА, в сторону направления угловой скорости ω 1. Скорость точки В определяется двумя способами:
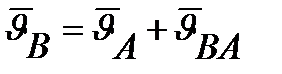 относительно т. А.
относительно т. А.
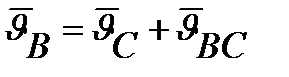 относительно т. В.
относительно т. В.
Следует задаться масштабом μV - масштаб скорости. Точка Р является полюсом плана скоростей. В ней сосредотачиваются все неподвижные точки механизма.
От точки Р откладываем вектор VА.
Величина определяется следующим образом:
Выбираем отрезок на чертеже, представляющий вектор скорости VА:
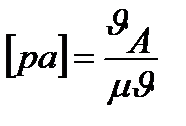 -выбираем произвольно, исходя из формата чертежа.
-выбираем произвольно, исходя из формата чертежа.
Направление отрезка  перпендикулярно звену ОА.
перпендикулярно звену ОА.
Из двух уравнений для вектора скорости VВ второе превращается в тождество, так VС=0, поэтому построение плана скоростей производим согласно первому уравнению, относительно точки А:
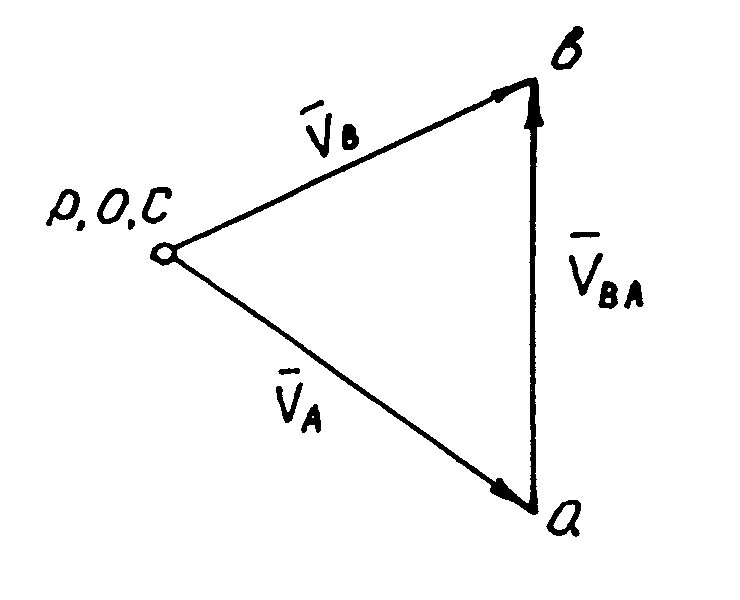 |
Рисунок 7.6 План скоростей
Скорость точки В неизвестна по величине, но известна по направлению, она ┴ звену ВС.
Вектор скорости VВА также неизвестен по величине, но известен по направлению, он перпендикулярен звену АВ.
Проведем две линии, одну через полюс Р по направлению вектора скорости VВ, вторую через конец вектора 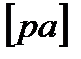 , по направлению вектора скорости VВА. Пересечение этих линии даст два вектора pв, а, которые представляют неизвестные свекторы скоростей VВ, VВА.
, по направлению вектора скорости VВА. Пересечение этих линии даст два вектора pв, а, которые представляют неизвестные свекторы скоростей VВ, VВА.
Согласно векторному уравнению получили графическое представление скоростей. Теперь в соответствии с ранее выбронным масштабом скорости μV, определим величину скоростей VВ, VВА. Она будут равны:
VВ=[рв] μV;
VВА= [ав]μV;
Также можно определить угловые скорости ω 2 и ω 3 .
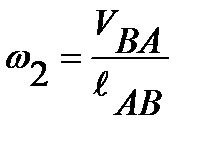 ;
; 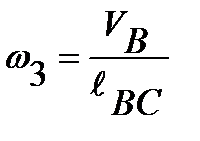 ; (7.13)
; (7.13)
Для определения направления ω2 перенесем вектор 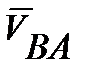 на звено АВ и посмотрим, как будет двигаться звено. Видно, что вектор угловой скорости ω2 направлен против часовой стрелки.
на звено АВ и посмотрим, как будет двигаться звено. Видно, что вектор угловой скорости ω2 направлен против часовой стрелки.
Теорема подобия планов скоростей (общие понятия)
При построении планов скоростей очень важно знать о подобии планов скоростей. Сформулируем эту теорему так:
Теорема подобия планов скоростей: отрезки прямых линий, соединяющие точки на схеме звена механизма, и отрезки прямых линий, соединяющие концы векторов относительных скоростей этих точек на плане скоростей, образуют полные и сходственно расположенные фигуры. Фигура на плане скоростей повернута относительно фигуры схемы звена на 90 градусов.
Литература: /1/ гл. 6, §32 /2/ гл2, лекция 6, /1/ гл. 6, §31 /2/ гл.2 лекция 5
1. Напишите векторное уравнение для каждой группы Ассура отдельно.
2. Как выбирается масштаб скорости?
3. Чем отличается планы скоростей для вращающейся и поступательной пары?
4. О чем гласит теорема подобия планов скоростей?
5. Что называют радиусом - вектором?
6. Напишите формулы для определения скорости и ускорения при:
- поступательном движении;
- вращательном движении;
- плоскопараллельном движении.
 2015-06-05
2015-06-05 2103
2103

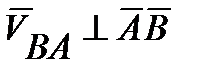 ,
,