Проблемы решения многокритериальных задач

Постановка и классификация многокритериальных задач

Многокритериальные задачи (МКЗ)

Исходными данными для МКЗ является матрица значений единичных критериев 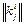, размерности 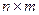, строками которой являются объекты (варианты) 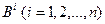, а столбцами – критерии .

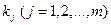Многокритериальные задачи различаются видом требуемого результата решения. В этой связи выделябтся следующие многокритериаль­ные задачи:

a) задачи, в которых необходимо выделить из множества объектов один наиболее предпочтительный объект (получить одно наиболее предпочтительное решение). В некоторых случаях может быть выделено не одно, а подмножество экви­валентных и наиболее предпочтительных объектов;

b) задачи, в которых необходимо упорядочить многокрите­риальные объекты. Например, упорядочить по предпочтению варианты технических систем, по качеству – образцы продукции;

c) задачи, в которых требуется дать оценку полезности (качества) объектов. Другими словами, необходимо построить функцию полезности .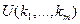

d) задачи, в которых требуется выделить подмножество эффективных (конкурирующих) объектов. Такие подмножества называют оптимальными по Парето.

Чтобы говорить об эффективных объектах, необходимо ввести понятие доминируемого объекта.

Определение 1.1. Объект 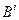доминирует объект 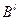, если по всем критериям 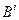предпочтительнее или эквивалентен 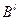и хотя бы по одному критерию строго предпочтительнее. Объект 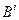называют доминирующим, а 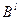– доминируемым.

Если исключить из исходного множества доминируемые объекты, то останутся конкурирующие (эффективные). На рис.1.2 на примере двух критериев дискретной МКЗ выделено подмножество 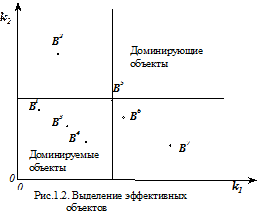эффективных объектов. В примере принято, что при увеличени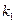и и 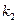возрастает предпочтение объектов, 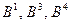– доминируемые объекты.

Следует подчеркнуть, что прежде чем задачу выделения наи­более предпочтительного объ­екта, необходимо сначала выделить подмножество эф­фективных объектов, так как искомый объект может на­ходиться только в этом под­множестве.

Задача выделения подмножества эф­фективных объектов решается просто, так как достаточно исключить из исходного множества доминируемые объекты.

Основная проблема в решении МКЗ заключается в неодно­родности пространства критериев, так как единичные критерии измеряются в различных единицах измерения. Поэтому в большинстве методов осуществляется переход от физических единиц к относительным единицам измерения , например, с использованием функций перевода. Процедуры перехода к относительным единицам отличаются в разных методах, поэтому они будут описаны при изложении методов.

Следует подчеркнуть, что проблема однородности простран­ства критериев не решается полностью только переходом к относительным единицам, так как сравнить два объекта в про­странстве критериев не представляется возможным. Поэтому необходимо также определить важность критериев (коэффициенты относительной важности) .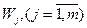

Коэффициенты 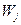задаются ЛПР (или экспертами) и отражают его структуру предпочтений.

Второй проблемой является агрегирование множества критериев в скаляр. В большинстве методов эта проблема решается тем или иным способом, но в некоторых методах она снимается путем введения определенного принципа выбора наиболее предпочтительного объекта (решения).

В отдельных методах проблемы неоднородности простран­ства критериев и агрегирования решаются путем сведения единиц измерения всех критериев к одной. Часто в экономи­ческих задачах такой единицей служит денежная единица (рубль). Тем самым стараются свести векторную многокрите­риальную задачу к скалярной.

Другой важной проблемой решения МКЗ является оценка доверия к получаемому решению. Дело в том, что при решении задач используется субъективная информация, поэтому у ЛПР возникает недоверие к результату.

Степень доверия к результату может быть оценена через его устойчивость по отношению к субъективным данным, использу­емым в методах (коэффициенты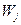, процедуры перехода к относительным единицам и т.д.) Если, например, при измене­нии 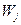в качестве наиболее предпочтительного выделяется один и тот же объект, т.е. результат устойчив по отношению к 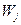,то доверие к выделенному объекту выше.

Следует особо сказать об исследовании устойчивости результата по отношению к используемым методам решения МКЗ. Так как в каждом из методов используются различные идеи (подходы), то и результаты решения одной и той же задачи разными методами могут отличаться. Если же при использовании нескольких методов выделяется один и тот же наиболее предпочтительный объект, т.е. результат устойчив по отношению к методам, то доверие к полученному решению, конечно, высокое.