Принятие решений в условиях риска. Принятие решений в условиях неопределенности

Принятие решений в условиях неопределенности

В этом случае нет данных о вероятностях исходов.

Для выбора варианта объема выпуска используются определенные принципы (критерии выбора). Рассмотрим их.

	И1	И2	И3	И4	И5	И6	Вальда	Гурвица (a= 0,6)	Лапласа
								24+4=28
								33+11,2=44,2	37,3
								36+7,2=43,2	40,8
								45+3,6=48,6
								54+1,6=55,6	54,5
Max

U_i,j – полезность варианта i при исходе j

Критерий Вальда:

Max (min U_i,j )

^{i j}

Критерий Гурвица:

Max [a*max U_i,j + (1 - a)*min U_i,j ],

^{i j j}

где a - коэфф. оптимизма.

Критерий Лапласа:

Max [ S U_i,j / n ]

ⁱ

Критерий Сэвиджа (сожалений):

Расчет сожалений производится в соответствии с выражением: S_i,j = max U_i,j - U_i,j

Критерий Сэвиджа ориентирован на лиц, которые очень сожалеют о том, что выбрали не самый лучший вариант. Критерий позволяет минимизировать сожаление.

Рассчитаем матрицу сожалений

	И1	И2	И3	И4	И5	И6	Максимум

Для определения наилучшего варианта используем критерий Вальда, но с матрицей сожалений.

ⁱ

Min (max S_i,j )

^{i j}

Рассмотрим свойство независимости решения от множества вариантов. Данное свойство выполняется для критериев. Вальда, Гурвица, Лапласа. Для критерия сожалений свойство не выполняется.

В этом случае известны вероятности исходов

Матрица для анализа рисков

Вероятности	0,1	0,15	0,25	0,25	0,15	0,1
	И1	И2	И3	И4	И5	И6	Мода	Мат. ожид	σ	М +а*s
									2,7	29,7
							30.5	34,8	1,7	36,5
							35,5	41,4	3,6
								46,2	6,1	52,3
								57,6	7,0	64,6

Оценка по моде – оценка по наиболее вероятному значению. В рассматриваемом примере максимальная вероятность 0.25 соответствует исходам 3 и 4. Поэтому в качестве оценки используем среднюю для И3 и И4.

Оценка по математическому ожиданию наиболее распространенная. Вспомните системы массового обслуживания. – характеристики СМО (среднее число заявок в системе, очереди, среднее время пребывания заявок в системе) оцениваются как их мат. ожидание.

В рассматриваемом примере мат. ожидание рассчитывается в соответствии с выражением:

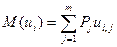
Оценка по мат.ожиданию и дисперсии производится с учетом как мат ожидания так и рассеяния значений (среднеквадратического отклонения σ):

М + а * s, где а = коэфф. риска

Если а > 0 – риск присутствует, а < 0 – риск уменьшается

Параметр а изменять в интервале [- M/2σ; M/2σ ], чтобы σ не было больше мат. ожидания

Возьмем а = 1

В₁ = 27 + 2,7 = 29,7

В₂ = 34,8 + 1,7 = 36,5

В₃ = 41,4 + 3,6 = 45

В₄ = 46,2 + 6,1 = 52,3

В₅ = 57,6 + 7 = 64,6