Упорядоченность кольца целых чисел

Доказательство.

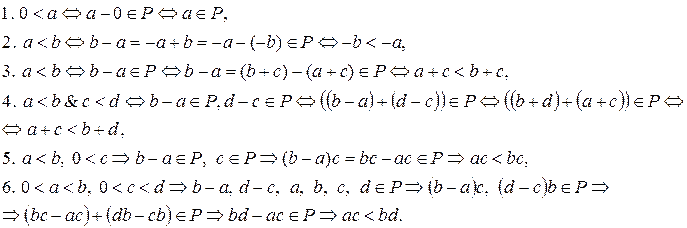что и требовалось доказать.

Теорема 8. Отношение ≤, определенное на упорядоченном кольце К с положительным конусом Р следующим образом: 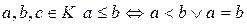, является линейным порядком.

(доказательство самостоятельно).

Теорема 9. Кольцо целых чисел 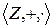является упорядоченным кольцом с положительным конусом N.

Доказательство.

Множество N является непустым подмножеством целых чисел, удовлетворяющих всем аксиомам положительного конуса.

что и требовалось доказать.

Следствие 1. Отношение < на множестве , определенное по правилу 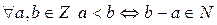, является строгим линейным порядком и выше указанным удовлетворяет свойствам 1.-6.

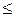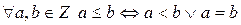Следствие 2. Отношение на множестве , определенное по правилу , является линейным порядком.