Доказательство. Теорема 15. , где b≠0, существует и при том единственная пара целых чисел такая, что

Теорема о делении с остатком.

Теорема 15. 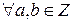, где b≠0, существует и при том единственная пара целых чисел 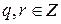такая, что 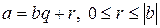. 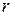назовем остатком при делении a на b, q – неполным частным.

Существование (?)

Проведем методом математической индукции в 3-ей форме.

1. База индукции.

Рассмотрим множество . Очевидно, это множество непустое и не ограничено сверху. Для любого элемента 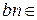В верна теорема о делении с остатком в разделе существования, поскольку b≠0, bn=bn+ 0, где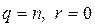,0≤<.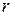

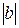2. Индуктивное предположение.

Предположим, что для произвольного целого числа z данная теорема справедлива, т.е. z = bq+r, где 0≤r<.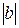

3. Проверим справедливость данного утверждения для числа z – 1.

z = bq+r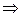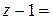bq+ (r– 1), где0 ≤r<.

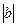Рассмотрим возможные случаи:

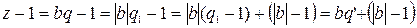, где 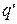- неполное частное, 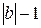- остаток, причем 0≤ <.

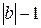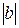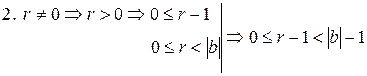. Тогда q, r– 1 – искомая пара чисел для 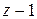и .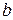

Существование доказано.

Единственность (?)

Методом от противного. Пусть 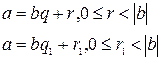. Тогда 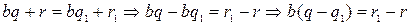. Учитывая, что 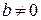, рассмотрим следующие случаи:

1. .

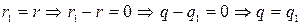2. 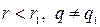. Тогда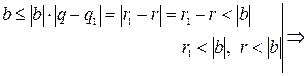 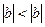- противоречие. Следовательно, такой случай невозможен.

3. 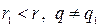. Невозможен, доказательство аналогично 2.

Таким образом, из трех случаев возможен только один 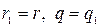. Единственность доказана.

что и требовалось доказать.