Доказательство. Архимедовская расположенность поля рациональных чисел

Архимедовская расположенность поля рациональных чисел.

Теорема 6. Поле рациональных чисел архимедовски расположенное, т.е. выполняется аксиома Архимеда: .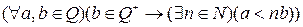

Пусть .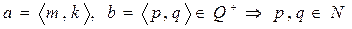

Заметим, что .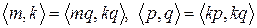

Поскольку кольцо целых чисел является архимедовски расположенным, имеем: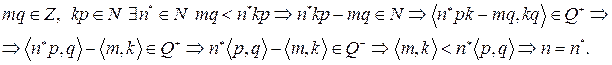

что и требовалось доказать.

Теорема 7. Поле рациональных чисел является всюду плотным.

Доказательство.

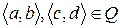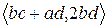Пусть . Для определенности положим, что . Покажем, что элемент лежит между указанными элементами, т.е. 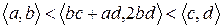. Докажем каждое из неравенств отдельно.

(?)

(?)

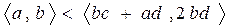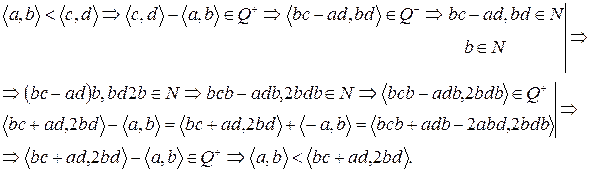
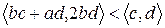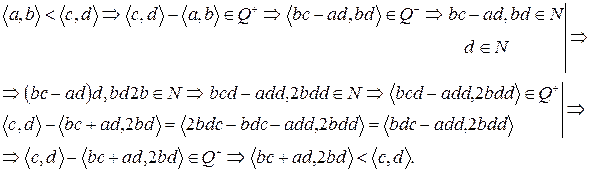
что и требовалось доказать.