Геометрическая интерпретация чисто мнимых кватернионов

Доказательство.

Свойства сопряженных и нормы.

Теорема 3. Для любых кватернионов 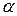и 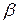справедливы следующие свойства:

1. ;

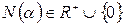2. ;

3. ;

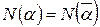4. ;

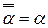5. ;

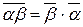6. ;

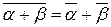7. ;

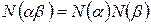8. Если 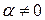, то .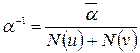

Пусть 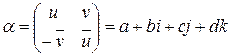и .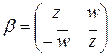

1. .

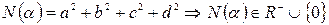2. .

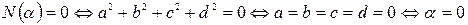3.

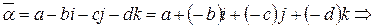
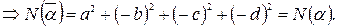
4. .

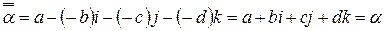5. , .

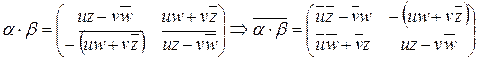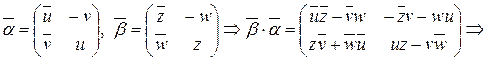
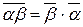6. Аналогично 5.

7. .

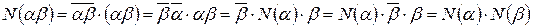8.

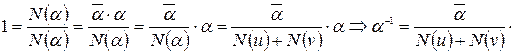
что и требовалось доказать.

Определение. Кватернион называется чисто мнимым, если его действительная часть равна нулю.

Если 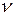- чисто мнимый кватернион, то .

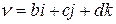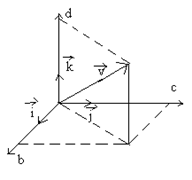
правая тройка:

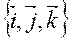- правоориентированный ортонормированный базис

Умножение чисто мнимых кватернионов:

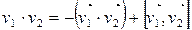, где 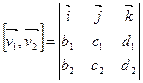, причем 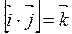, , 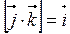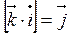. Докажем эту формулу:

.

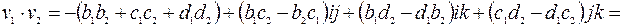
Следствие. Произведение чисто мнимых кватернионов является чисто мнимым т.т.т. когда соответствующие им вектора взаимно перпендикулярны.