(ассоциативные алгебры над полем действительных чисел размерности 2).
Опишем все ассоциативные алгебры над полем 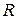 размерности 2.
размерности 2.
Нетрудно устанавливается, что множества 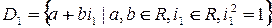 и
и 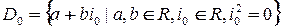 образуют ассоциативные алгебры, которые договоримся называть алгебрам двойных чисел и дуальных чисел соответственно.
образуют ассоциативные алгебры, которые договоримся называть алгебрам двойных чисел и дуальных чисел соответственно.
Теорема. Любая коммутативная ассоциативная алгебра с единицей над полем действительных чисел 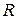 размерности 2 изоморфна одной из из алгебр
размерности 2 изоморфна одной из из алгебр 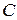 ,
, 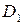 ,
, 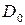 .
.
Доказательство
Пусть 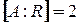 , где
, где 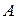 - коммутативная ассоциативная алгебра с единицей
- коммутативная ассоциативная алгебра с единицей 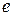 . Рассмотрим
. Рассмотрим 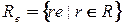 . Нетрудно устанавливается, что
. Нетрудно устанавливается, что 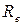 изоморфно полю
изоморфно полю 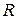 . Тогда, с точностью до изоморфизма, можно утверждать, что
. Тогда, с точностью до изоморфизма, можно утверждать, что 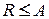 (
(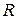 подполе поля А). Последнее означает, что в
подполе поля А). Последнее означает, что в 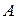 найдется элемент
найдется элемент 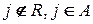 такой, что система
такой, что система 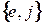 образует базис алгебры
образует базис алгебры 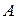 над полем
над полем 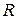 .
.
 для некоторых
для некоторых 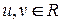 .
. 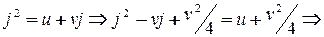
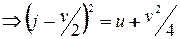 . Возможны случаи:
. Возможны случаи:
1. 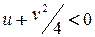 . Существует положительное действительное число
. Существует положительное действительное число 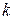 такое, что
такое, что 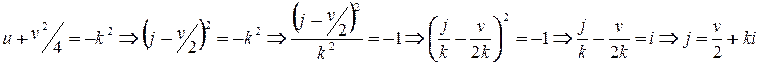
Тогда 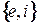 - система порождающих в
- система порождающих в 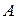 . Покажем, что
. Покажем, что 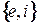 - базис в
- базис в 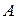 . Предположим, что
. Предположим, что 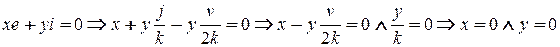 . Таким образом
. Таким образом 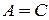 .
.
2. 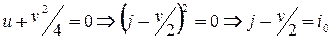 . Аналогично устанавливается, что
. Аналогично устанавливается, что 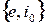 - базис в
- базис в 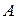 . Следовательно,
. Следовательно, 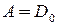 .
.
3. 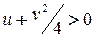 . Существует положительное действительное число
. Существует положительное действительное число 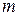 такое, что
такое, что 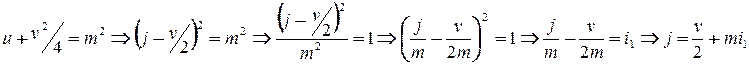
Тогда 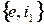 - система порождающих в
- система порождающих в 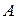 . Аналогично устанавливается, что
. Аналогично устанавливается, что 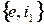 - базис в
- базис в 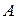 . Следовательно,
. Следовательно, 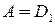 .
.
Замечание. Наличие единицы 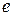 позволяет включить
позволяет включить 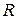 в
в 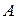 , а ассоциативность и коммутативность позволяют выполнять действия, указанные выше.
, а ассоциативность и коммутативность позволяют выполнять действия, указанные выше.
что и требовалось доказать.
Теорема. Алгебры 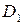 ,
, 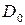 не являются полями.
не являются полями.
Доказательство
Предположим, что элемент 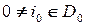 обратим. Тогда существует элемент
обратим. Тогда существует элемент 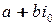 такой, что
такой, что 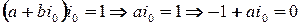 . Последнее противоречит линейной независимости элементов
. Последнее противоречит линейной независимости элементов 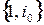 . Следовательно, предположение об обратимости элемента
. Следовательно, предположение об обратимости элемента 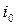 оказывается ложным, а, значит,
оказывается ложным, а, значит, 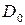 не является полем.
не является полем.
Аналогично устанавливается необратимость элемента 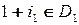 . Тогда
. Тогда 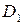 также не является полем.
также не является полем.
что и требовалось доказать.
Теорема. Алгебры 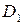 ,
, 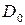 существуют.
существуют.
Доказательство
 . Тогда
. Тогда 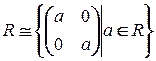 ,
, 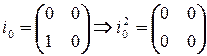 . Таким
. Таким
образом 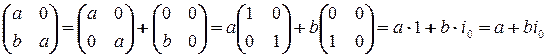 .
.
 . Тогда
. Тогда 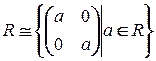 ,
, 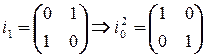 . Таким
. Таким
образом 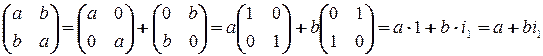 .
.
что и требовалось доказать.
Замечание. Алгебры 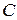 ,
, 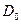 и
и 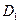 являются подалгебрами алгебры
являются подалгебрами алгебры 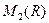 .
.
 2014-02-02
2014-02-02 649
649








