2014-02-02
2374
Теорема Фробениуса.
Теорема Фробениуса. Единственными с точностью до изоморфизма конечномерными ассоциативными алгебрами с делением над полем действительных чисел являются алгебры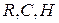 
.
Пусть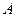 
- конечномерная ассоциативная алгебра с делением над полем действительных чисел и 
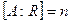. Возможны случаи:
1. 
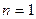. Тогда 
.
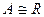2. 
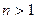. Тогда в алгебре 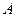есть хотя бы один элемент, который не является действительным числом. Обозначим этот элемент через 
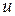. В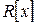 
существует неприводимый многочлен 
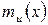, корнем которого является 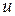. Поскольку наивысшая степень неприводимого многочлена с действительными коэффициентами над полнм действительных чисел равна 2 и элемент 
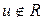, а, значит, не может быть корнем ни непостоянного многочлена, ни многочлена первой степени, то 
.
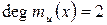Пусть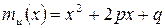 
. Так как 
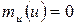, то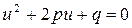 
. Выделим полный квадрат в левой части. Получим 
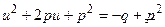. Поскольку многочлен 
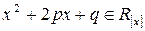неприводим, то 
.
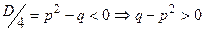Рассмотрим число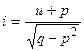 
, причем 
, 
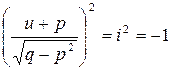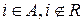. Тогда в алгебре 
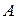система 
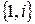является линейно независимой, а, значит,
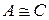в случае 
.
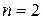3. 
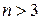. Тогда в алгебре 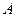найдется еще один элемент 
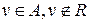такой, что система 
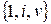линейно независима и 
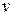- корень подходящего неприводимого многочлена 
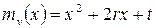второй степени. Аналогично пункту 2 формируется элемент 
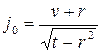, который также удовлетворяет условиям 
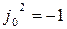и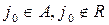 
.
Поскольку 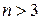система 
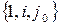линейно независима.
Рассмотрим пару элементов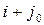 
и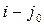 
. Оба элемента не принадлежат полю действительных чисел, а, значит, является корнями неприводимых над полем действительных чисел многочленов с действительными коэффициентам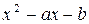и 
и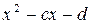 
соответственно. Тогда
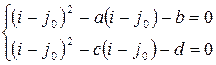
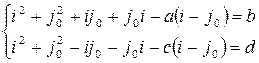
Заменив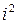 
и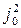 
на -1 и сложив уравнения системы, получим
.
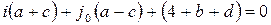Поскольку 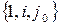система линейно независима, то 
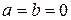и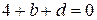 
. Возвращаясь к исходному соотношению, получим 
.
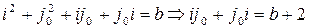Введем число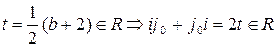 
. Рассмотрим число
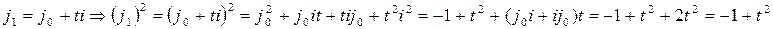
Зная, что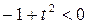 
, введем число 
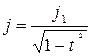. Поскольку 
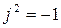система 
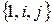линейно независима. Вычислим 
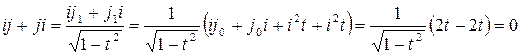. Таким образом получается, что нашлась линейно независимая система 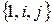такая, что 
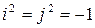и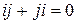 
.
Обозначим через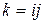 
. Покажем, что система 
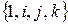линейно независима. Поскольку ранее установлена линейная независимость 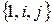, то остается показать, что 
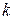линейно не выражается через 
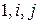. Предположим, что 
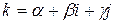, где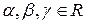 
.
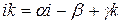, так как 
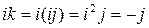. Тогда
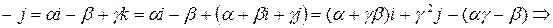
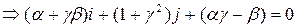, где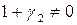 
. Последнее противоречит линейной независимости элементов 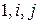, следовательно, 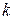линейно не выражается через 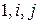и система 
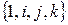линейно независима.
Нетрудно проверяется, что элементы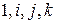 
относительно умножения образуют следующую таблицу:
 |  |  | | |
| | | | | |
| | |  | |  |
| | |  | | |
| | | |  | |
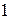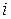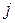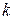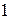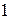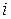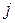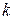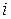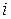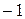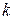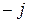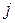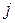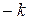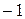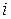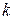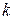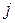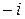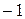Например, 
.
Таким образом, 
в случае 
.
4. 
. Тогда существует элемент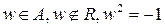 
.
Предположим, что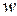 
линейно не выражается через 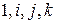, т.е. 
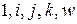- линейно независима. Пусть 
.
Найдем произведение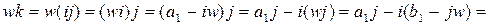 
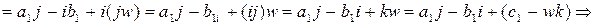
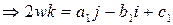. Умножим последнее равенство на 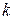. Получим 
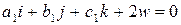, где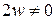 
, что противоречит линейной независимости системы 
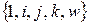. Следовательно, система 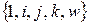линейно зависима.
Таким образом, 
не может быть больше 4, а, значит, размерности всех конечномерных алгебр над полем действительных чисел совпадают с одним из чисел 1, 2, 4.
что и требовалось доказать.
