2014-02-02
1523
Лекция 12.
Доказательство.
Если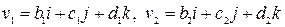 
, то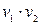 
является чисто мнимым кватернионом т.т.т. когда 
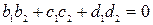, а последнее выполняется т.т.т., к. 
.
что и требовалось доказать.
Определение. Алгеброй А над полем К или К -алгеброй называется линейное пространство А над полем К, в котором определена бинарная операция умножения векторов, удовлетворяющая следующим аксиомам:
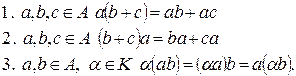
Определение. Алгебра А над полем К называется ассоциативной, если
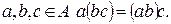
Определение. Алгебра А над полем К называется коммутативной, если
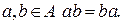
Определение. Алгебра А над полем К называется алгеброй с делением, если
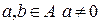разрешимы уравнения 
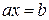и 
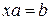
Определение. Рангом алгеброй А над полем К называется размерность линейного пространства А над полем К в случае его конечномерности.
Примеры:
1. 
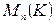- алгебра квадратных матриц n -ого порядка над полем К, где 
.
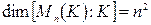2. 
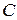- алгебра над полем R, где 
.
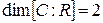3. 
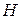- алгебра над полем 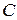, где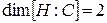 
.
Определение. Алгебры А и В над полем К называются изоморфными, если существует биективное отображение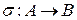 
,удовлетворяющее условиям:
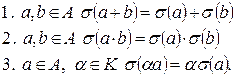
Пример. Алгебра квадратных матриц n -ого порядка над полем К илинейное пространство линейных операторов n -мерного линейного пространства над полем К (каждому оператору можно поставить в соответствие его матрицу в некотором фиксированном базисе).
