Раздел 2.
Классификация САУ.
Методов исследования САУ много и имеется следующая их классификация, учитывающая способы математического описания.
 |

 САУ
САУ
| По виду уравнений САУ. По характеру передачи сигнала. По характеру процессов в системе. По критерию качества. |
 |  |
Стационарные Нестационарные
 |  |  | |||


Линейные Нелинейные
 |
Непрерывные Дискретные



Цифровые Импульсные
 |



Детерминированные Стохастические

 |  |  |
С заданным качеством Оптимальные Адаптивные
В первой (классической) части курса рассматриваются стационарные линейные непрерывные системы с заданным качеством. Под заданным качеством понимается обеспечение требуемых инженерных показателей по принципу “не хуже заданного”.
Лекция 2
Непрерывные, линейные, детерминированные модели систем управления.
 u(t) O y(t) u(t) O y(t)   |
u(t)=(u1(t)...um(t))T
y(t)=(y1(t)...yp(t))T
Может показаться, что моделью такого объекта может быть сложная нелинейная функция:
F(y,u)=0 (*)
На самом деле, такая функция часто не может описать объект. точнее, его динамику.
В соответствии с теоремой Юнга о неявно заданной функции, можно выразить:
yi = j(y1,... кроме yi, yp, u)
Нетрудно видеть, что ступенчатое изменение входного сигнала u приводит к ступенчатому же изменению выходного сигнала, т.е. отсутствуют переходные процессы. Поэтому для рассмотрения объектов имеющих переходные процессы необходимо использовать более сложные модели.
F(y¢, y¢¢,... y(n), u¢, u¢¢,... u(m))=0 (**)
- это наиболее общий вид нелинейного дифференциального уравнения, связывающего входной и выходной сигнал. Так как y и u, в свою очередь, являются векторами, то на самом деле (**) есть система нелинейных дифференциальных уравнений.
Существует два способа получения д.у. объекта:
1.Способ известных законов (закон Ома, законы механики и т.д.)
Применим в двух случаях: когда объект управления простой и система невысокого порядка. Или когда объект очень сложный и в следствии его сложности можно воспользоваться законами статистики.
2. Эвристический способ. Заключается в том, что вместо использования готовых законов, уравнения не вытекающие ни из каких законов предлагаются из опыта работы с предыдущими объектами и пр. Такое описание называют феноменологическим, т.е. описание объекта по основным чертам его внешнего поведения, без глубокого проникновения в сущность его функционирования. Полученная таким образом модель должна быть исследована на адекватность, т.е. насколько она соответствует требованиям. Далее следует проверка границ адекватности.
Построим модель водоема с карасями. Пусть в нем водится рыба, которая вылавливается с интенсивностью П.
x - количество рыбы.
П - интенсивность вылова, в единицу времени.
dx = k*x*dt - Пdt
k - коэффициент размножения, является функцией от x
k = k(x)» k0 + k1*x +... внимание!!! – это эвристическое выражение
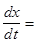 (k0 + k1*x)x -П - дифференциальное уравнение.
(k0 + k1*x)x -П - дифференциальное уравнение.
k0 - пропорционально количеству рыбы
k1 x - пропорционально скорости роста рыбы
Упростим дифференциальное уравнение по формулам:
                  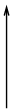   z c<1/4 z2 z1 t z 0.5 c>1/4 z c<1/4 z2 z1 t z 0.5 c>1/4  t t      z t z t |
t = t*a
z = x/b
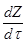 = (1-z)z - c
= (1-z)z - c
a = 1/k0 b = k0/k1 c = П/k1
Видим, что полученная модель описывает интересные эффекты – стабилизация количества рыбы при умеренном вылове С и при достаточном начальном количестве z.
Напротив, караси вымирают за конечное время, если их было мало или ловили слишком много.
В данном примере дифференциальное уравнение получилось нелинейным. Только в следствии его крайней простоты удалось получить решение и в последствии попытаться разработать регулятор. Однако, для общих нелинейных дифференциальных уравнений этого сделать не удается и модель объекта приходиться упрощать. Единственным классом дифференциальных уравнений поддающимся эффективному исследованию, является линейное дифференциальное уравнение с постоянными коэффициентами и системы таких уравнений. В этом случае уравнение (**) примет следующий вид:
A0y(n) + A1y(n-1) +... +Any = B0u(m) + B1u(m-1) +... +Bnu (1)
Обозначим:
M = Bm + Bm-1 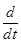 +... +B0
+... +B0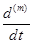
и соответственно:
N = An + An-1 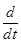 +... +A0
+... +A0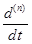
Уравнение (1) примет вид:
N*y = M*u
 2014-02-02
2014-02-02 1118
1118
