Основным методом исследования линейных систем с постоянными коэффициентами является метод преобразования Лапласа

Мы не будем здесь подробно излагать свойства преобразования Лапласа, отметим лишь наиболее важные для ТАУ свойства.

При нулевых начальных условиях, после преобразования Лапласа уравнения (4), получаем: L{(4)}:

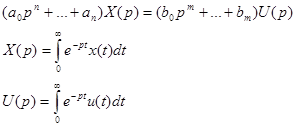
Преобразования Лапласа выходного сигнала X(p), отнесенное к преобразованию Лапласа входного сигнала U(p) не зависит от самих сигналов. Это свойство самого объекта.

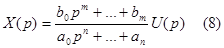
Передаточная функция

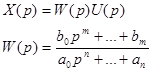
(9)

Определение: Передаточной функцией системы (объекта) называется отношение преобразования Лапласа выходного сигнала к входному при нулевых начальных условиях.

Порядок системы – порядок полинома знаменателя передаточной функции

Передаточная функция W(p) зависит только от самих дифференциальных уравнений

Передаточная функция W(p) определена только для линейных уравнений и выражает свойство линейности: если U= U₁+U₂, то, очевидно:

X(p)=W(p) (U₁+U₂)= W(p) U₁+ W(p) U₂ = X₁(p) + X₂(p)

X(p)=W(p) (g U₁)= g W(p) U₁

Например, устройство, вычисляющее модуль входного сигнала или квадрат входного сигнала непосредственно не описывается передаточной функцией (почему?).