Переходной функцией объекта называется реакция на единичную ступеньку на входе при нулевых начальных условиях

Гармоническое входное воздействие. sin wt

sin wt = Im e^jwt т.к. e^jwt =cos wt + j cos wt

L(sin wt) = L(Im e^jwt) = Im L(e^jwt) = Im (1/(p-jw)) = Im((p+jw)/(p²+w²)) =

Im(p/(p²+w² )+jw/ (p²+w²)) = w/ (p²+w²)

5. d - функция (модель очень короткого, конечного воздействия большой мощности)

Определение d - функции:

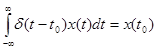
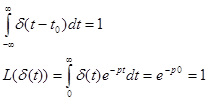
Замечание:

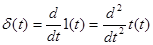
Определение 1:

H(t) – переходная функция.

H(p)=W(p)/p

Определение 2:

Весовой функцией (импульсной переходной функцией блока), называется реакция на d - функцию на входе при нулевых начальных условиях.

h(p)=W(p) 1=W(p) (*)

Очевидно, что h(p)=pH(p), или

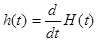
Заметим, что произведение изображений соответствует свертке:

т. к. Y(p)=W(p)U(p)

И т.к. W(p)=h(p) то:

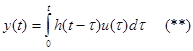
Выходной сигнал в каждый момент времени зависит не только от входного сигнала в этот момент времени, но и от входа во все предыдущие моменты времени. При этом с “весом”, определенным функцией h.

Из (**) и из (*) вытекает следующая схема проведения эксперимента по определению параметров звена (блока):

1) Пусть d^*(t)»d(t) (т.к. d(t) физически не реализуема) то: h^*(t)»h(t)

2) L(h^*(t))=W^*(p)»W(p)

Другой подход: На вход подаем 1(t)

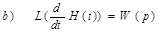
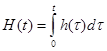
a) Измеряем H(t)

Замечание:

Численное дифференцирование – некорректная операция (с точки зрения вычислительных методов).