Типовые звенья САУ

Раздел 3.

Полиномы числителя и знаменателя передаточной функции можно разложить на простейшие множители по их корням .

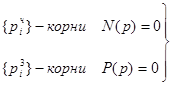множество корней числителя и знаменателя.

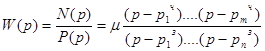здесь : m = b₀/a₀ – константа.

Возможны 2 случая :

а) Корни вещественные. Оставляем скобки без изменения.

б) Пара комплексно сопряженных корней вида : p_1,2=a ± j *b - объединяем их и раскрываем скобки

(p-a+jb)(p-a-jb)= p²-2a p + b² + a²

где p²-2a p+b ²+a ² – имеет вещественные коэффициенты .

После такого представления в числителе и знаменателе будет некоторое количество скобок первого порядка , соответствующих вещественным корням и некоторое количество скобок второго порядка , соответствующим комплексно – сопряженным корням . При этом все числовые коэффициенты в скобках будут вещественными.

Рассмотрим каждую такую скобку как элементарную передаточную функцию.

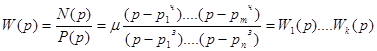k=n+m, если все корни вещественные

k<n+m, если есть комплексные корни

Принято выносить общий множитель за скобки так , чтобы свободный член всех скобок был равен 1 .

Можно заметить , что для любого W_i (р) может быть :

1) к – усилительное звено

2) p – дифференциальное звено

3) 1/p – интегральное звено

4) k/(T_p+1) – инерционное (апериодическое звено)

5) k/(T²p²+2dTp+1) – колебательное звено

6) k*(Tр+1) – форсирующее звено

7) (T²p²+2dTp+1) - форсирующее звено 2-го порядка

1), 2), 3), 4), 5), - типовые звенья ТАУ.

6).форсирующее звено является комбинацией (суммой) усилителя и дифференциатора.

7). не является в строгом смысле реализуемым звеном (впрочем, как и 2, и 6 ).