Спектром периодической функции являются отдельные точки

Передаточной функции для системы дифференциальных уравнений (5,6) соответствует преобразование Лапласа для векторных сигналов, рассматривается абсолютно аналогично с учетом некоммутативности матриц.

Лекция 6

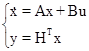
Рассмотрим систему чуть более общу, чем (6), она

отличается от (6) тем, что в данном случае может быть

многомерный вход и многомерный выход

А – матрица (m*n)

B – матрица (n*k)

H – матрица (p*n)

U – k-мерный вектор

Y – p-мерный вектор

Делаем преобразование Лапласа: (при 0 начальных условиях!!!)

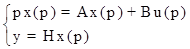
(pE-A)x(p)=Bu(p)

x(p)=(pE-A)^-1Bu(p)

Y(p)=H(pE-A)^-1Bu(p) где H(pE-A)^-1B – есть W(p)

Определение 3:

Частотной характеристикой блока с передаточной функцией W(p) называется комплексно – значная функция вещественного аргумента W(jw), т.е. при подстановке p= jw

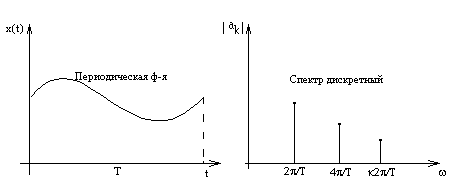
Покажем, какая имеется связь между спектром сигналов в системе, частотной характеристикой и преобразованием Лапласа.

Спектром периодической ф-ии является набор ее коэффициентов Фурье. Если имеем периодическую функцию с периодом Т, то коэффициент Фурье а_к вычисляется по формуле

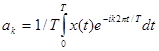
При увеличении периода Т, спектр становится гуще.

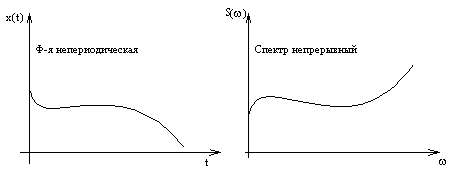
Для непериодической функции спектр превращается в непрерывный:

При устремлении T в бесконечность, ряд Фурье переходит в интеграл Фурье, а коэффициенты Фурье переходят в преобразование Фурье по следующей формуле:

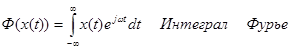
Интеграл Фурье следует понимать, как разложение Фурье x(t) по непрерывным частотам.

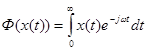
Т.к. x(t)є0 при t < 0, то

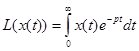
Вывод: Подстановка p=jw в изображение по Лапласу произвольной функции, превращает преобразование Лапласа в спектр, или что то же самое, в преобразование Фурье.

Y(p)=W(p)U(p) p=jw

Y(jw)=W(jw)U(jw) (***) Явно описывает изменение спектра при прохождении через блок с передаточной функцией W(p)

Из (***) следует,что при подаче на вход простого гармонического сигнала U(t)=sin wt, выходной сигнал в установившемся режиме будет гармоническим с изменившимися амплитудой и фазой.

U(t)=e^jwt

Y(t)=A(w)e^j(wt+j(w))=A(w)e^jj(w) e^jwt

W(jw) =Y(jw)/U(jw)= A(w)e^jj(w) e^jwt / e ^jwt = A(w)e^jj(w) =ъ W(jw)ъ e^{i arg W(jw)}

Где ъ W(jww)ъ - АЧХ -Амплитудно–частотная характеристика

Arg W(jw) - ФЧХ -Фазочастотная характеристика

W(jw) - АФЧХ -Амплитудно–фазо–частотная характеристика

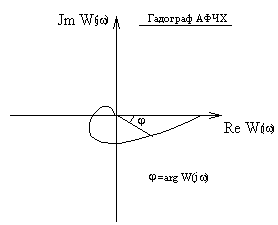
Частотные характеристики показывают амплитуду и фазу установившегося гармонического сигнала на выходе при поступлении на вход гармонического сигнала единичной амплитуды.