Вие является содержательным, отличая систему 3 порядка от 2 и 1

Общее решение системы линейных дифференциальных уравнений или линейного дифференциального уравнения высокого порядка (эти понятия сводятся друг к другу) выражается в виде суммы общего решения однородного уравнения (с 0 правой частью) и частного решения неоднородного уравнения. При тех сигналах, которые имеются в САУ, частное решение обычно имеет простой вид, не влияющий на устойчивость. Следовательно, вопрос устойчивости,- это вопрос устойчивости однородного уравнения.

Решение однородного уравнения выражается через корни характеристического уравнения и коэффициенты перед экспонентами, которые могут быть вычислены через вычеты:

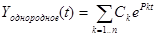,здесь р_к – корни характ. уравнения n-го порядка

Из этой формулы делаем основной вывод: чтобы переходный процесс заканчивался, -

· необходимо и достаточно, чтобы вешественные части корней р_к характеристического. уравнения n-го порядка были отрицательные, в этом случае имеются затухаюшие по экспоненте решения.

Для проверки этого факта (эквивалентного, конечно, устойчивости) имеется целый ряд критериев. Разница между этими критериями заключается в том, каким именно образом проверяется расположение корней в левой полуплоскости. Это можно сделать тремя способами:

· вычислив корни непосредственно, что бывает непростой вычислительной задачей;

· связав расположение корней с коэффициентами характеристического уравнения, что возможно, но трудности быстро возрастают с ростом порядка;

· судить об устойчивости по частотным характеристикам замкнутой или разомкнутой САУ.

Первые два способа называются алгебраическими, последний –третий,- частотным.

Алгебраические методы исследования устойчивости

· Необходимое условие устойчивости.

Если корни х.у. лежат в левой полуплоскости (система устойчива), то все коэффициенты х.у. имеют один знак:

Р(р) = a₀xⁿ + a₁x^n-1 +…+ a_n = 0; { a_k ><0 }

Равенство 0 недопускается (граница устойчивости)

Например: p² – p + 1 – неустойчивый полином;

3p³ + p² - p + 1 – также неустойчивый.

Однако, p² + p + 1 – устойчивый полином;

но(!) 3p³ + p² + p + 1 – по -прежнему неустойчивый (проверьте!)

Приведённый пример показывает, что данное условие – в самом деле, лишь необходимое, но не обязательно достаточное.

Область его применения – отсеивание заведомо неустойчивых систем.

· Необходимое и достаточное условие. Критерий Гурвица

(Адольф Гурвиц, Цюрих 1895г.)

При условии a_k >0 (это условие легко изменить на противоположное) для устойчивости необходитмо и достаточно выполнения n неравенств: Г_k > 0 при к = 1,..,n, где n – порядок полинома (системы), а Г_к:

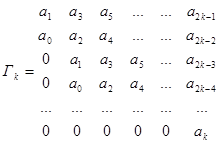Г_к >0

В первой строке каждого определителя находятся нечётные коэффициенты уравнения. Во второй строке – чётные. Далее идёт сдвиг на одно место вправо и т.д. В итоге имеется n определителей, которые являются главными диагональными минорами самой большой матрицы Гурвица Г_n (рассматртваемой не как определитель, а как матрица).

Сложности использования критерия Гурвица быстро возрастают с ростом порядка полинома, Эффективно возможно использование критерия до n <5.

Рассмотрим простейшие случаи.

· n = 1: a₁ >0, что в совокупности с а_к >0 не даёт ничего нового.

· n = 2: a₁ >0;a₁ a₂ - a₀ a₃ >0 в совокупности с а_к >0 не даёт ничего нового, так как а₃ =0 (его просто нет в уравнении 2 порядка)

· n = 3: a₁ >0; a₁ a₂ - a₀ a₃>0; a₃ Г₂ = a₃(a₁ a₂ - a₀ a₃) > 0.

В этих трёх условиях 1 и 3 не дают ничего нового, а второе усло-

Возвращаясь к примеру на предыдущей странице, становится понятно, почему полином 3p³ + p² + p + 1 является неустойчивым.

Заметим, что существует целый ряд модификаций критерия Гурвица, в том числе, и существенно упрощающих вычисления, например, критерий Рауса.

Доказательство критерия Гурвица-Рауса мы не приводим, так как оно достаточно сложное