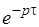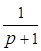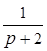D А - запас по амплитуде

Понятие запаса устойчивости по амплитуде и фазе.

Лекция 14

При выполнении условий критерия Найквиста годограф может при этом не охватывать точку (-1; j0) “ с запасом”. Оценим этот запас. Рассматривается отдельно запас по амплитуде и по фазе.

D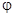- запас по фазе.

Im

D А

-1 1 Re

w=0

D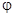

Запас по амплитуде означает, что при увеличении коэффициента усиления на D А система станет неустойчивой.

Аналогично, при появлении дополнительного фазового сдвига D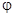 система также станет неустойчивой. Разные причины могут влиять на запасы устойчивости. В процессе проектирования гарантируются запасы устойчивости не ниже заданных. Таким образом, запасы устойчивости есть данные на проектирование САУ. Нетрудно видеть, что выразить запасы устойчивости можно также и на языке ЛАЧХ и ФЧХ.

Тогда определяются DL_дб = 20lg (DА) и Dj.

L_дб

ЛАЧХ

1

j DL w_дек

0

ФЧХ

-p/2

Dj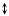

-p

Влияние звена чистого запаздывания на запас устойчивости.

Из-за времени распространения сигнала вдоль длинных линий, а также из-за времени вычисления в управляющих контроллерах возникают временные задержки сигналов без искажения их формы.

x (t)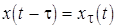

=; ; ;

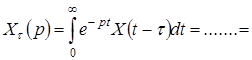
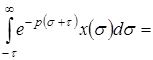
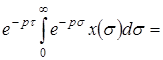
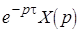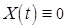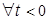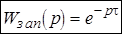
Таким образом, звену чистого запаздывания с постоянным временем запаздывания можно поставить в соответствие передаточную функцию.

Так как функция не дробно-рациональная, то и вся система не поддается простому исследованию с использованием корней характеристического полинома, так как полином становится 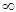порядка.

Рассмотрим пример. Вначале считаем, что t = 0. (нет запаздывания)

;

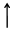
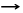
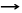
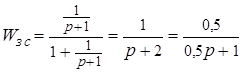Рассмотрим характеристическое уравнение замкнутой САУ.

Без запаздывания Р(р)_зс = 0.5р + 1, система, конечно, устойчива.

При наличии запаздывания t ¹ 0

; .

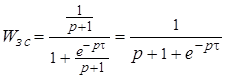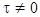Р(р)_зс = 0.5р + 1 + e^-pt Найти корни такого трансцендентного уравнения затруднительно, их, кроме того, бесконечное число. Но при больших t имеются корни с положительной вещественной частью (неустойчивость).