U-вектор входа

U=(u₁(t)… u_m(t))^T

Y=(y₁(t)… y_p(t))^T

X- вектор состояния.

x=(x₁(t)… x_n(t))

n – порядок дифференциального уравнения объекта.

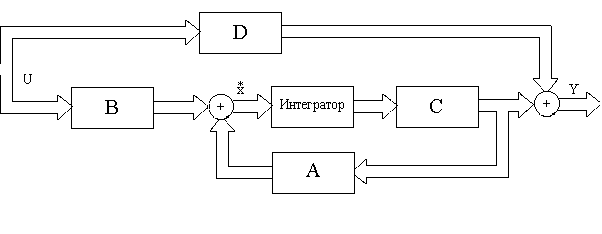
А – матрица (nxn)

В – матрица (nxm)

C – матрица (pxn)

D – матрица (pxm)

Замечание: В рамках системы (1) чрезвычайно удобно описывать нестационарные т.е. зависящие от времени объекты. При этом матрицы A,B,C,D. Зависят от времени, что соответствует переменным коэффициентам дифференциальных уравнений.

Замечание: В системе (1), второе уравнение также можно понимать как уравнение, описывающее косвенное измерение величины x некоторым датчиком.

Системе (1) соответствует передаточная матрица, которая также пери нулевых начальных условиях может быть вычислена при помощи преобразований Лапласа.

PX=AX+BU

Y=CX+DU

(pE-A)X=BU

X=(pE-A)^-1BU

Y=C(pE-A)^-1BU+DU=[C(pE-A)^-1B+D]U

Где [C(pE-A)^-1B+D] – передаточная матрица W(p)