Фильтр Винера является частным случаем фильтра Калмана (Ричард Калман), то есть многомерного нестационарного линейного оптимального фильтра

Имеются формулы, позволяющие получить передаточную функцию оптимального фильтра Винера, наилучшим образом решающую задачу.

Фильтр Калмана.

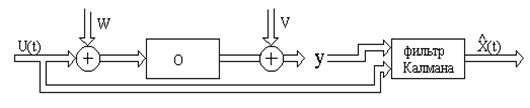
Постановка задачи: Имеется многомерная нестационарная линейная система, в которой имеются помехи W – в канале управления и V – в канале измерения. Кроме того, состояние объекта непосредственно недоступно измерению, а лишь косвенно с помехой V.

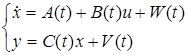- уравнения измерения

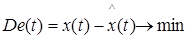Построить фильтр, чтобы

Требуем, таким образом, минимальной дисперсии ошибки фильтрации.

Предположим, что V и W (помехи) являются “белыми шумами” с нулевым математическим ожиданием, с заданными интенсивностями - дисперсиями и независимы между собой. Использовав подход похожий на построение наблюдателя, будем искать уравнение фильтра в следующем виде:

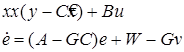Рассмотрев неизвестную матрицу G как параметр оптимизации, а дисперсию ошибки как критерий оптимизации и решив эту задачу оптимизации, получаем следующее выражение:

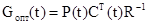R - матрица интенсивности шума.

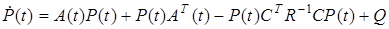Q - интенсивность шума W.

Таким образом оптимальный фильтр Калмана, даже при постоянных параметрах объекта, является системой с переменными коэффициентами. Поэтому, его затруднительно реализовать. Однако P(t) обычно быстро стремится к установившемуся значению и квази-оптимальный фильтр получается из оптимального, если мы выбираем G_опт=G_уст из условия: dP_уст /dt =0, что приводит к алгебраическому матричному уравнению для P_уст.

Фильтр Винера как раз соответствует стационарному установившемуся режиму работы фильтра Калмана.

Теорема разделения в задаче фильтрации.