Взаимная коррел. функция сигналов X и Y

Математическое ожидание,

т.к. плотность в разные моменты разная то и M(t) разное.

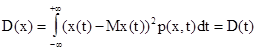- дисперсия.

М(t) и D(t) характеризуют значение x(t) в отдельные моменты времени.

-корреляционная функция.

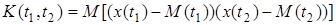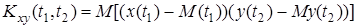Отметим, что K(t,t), т.е. t₁=t₂ это есть дисперсия в момент времени Dx(t). Корреляционная функция описывает статистическую связь значений процессов в разные моменты времени.

Стационарным случайным процессом называется такой случайный процесс, для которого корреляционная функция, на самом деле, зависит не от абсолютных значений t₁ и t₂, а только от их разности.

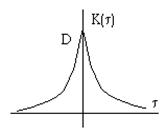Для стационарных случайных процессов: K(t₁ ,t₂) = K(t₁ -t₂) = K(t).

Типичный график корреляционной функции.

Для стационарного процесса математическое ожидание и дисперсия также не зависят от времени.

Стационарный случайный процесс для САУ не меняет своих статистических характеристик за время жизни системы.

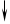Такие функции как M, D, K могут быть получены экспериментально. Будем считать, что в САУ помехи могут быть в двух основных местах: в канале управления и в измерителе.

W - помеха в канале управления.

V - помеха в канале измерения

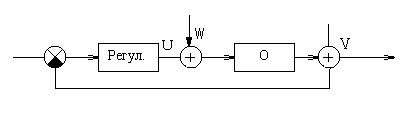
Спектральная плотность S(w) стационарного случайного процесса, есть интеграл Фурье:

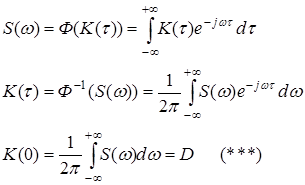Аналогично можно дать определение взаимной спектральной плотности двух процессо X и Y:

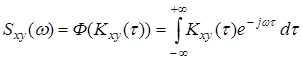из (***) видно, что дисперсия есть суммарная энергия случайного процесса. Чем больше дисперсия, тем больше энергия этого (“вредного”) сигнала.

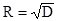- интенсивность, или среднеквадратическое отклонение.

Если рассмотреть сигнал с бесконечным равномерным спектром, то ему будет соответствовать корреляционная функция в виде d-функции. Т.е.:

S(w) = const

K(t) = (const/2p)*d(t)

D=K(0)=¥

Эти три уравнения есть “белый шум” с интенсивностью const/2p.

Реально “белый шум” всегда ограничивается по полосе пропускания системой и поэтому бесконечная дисперсия физического значения здесь не имеет. Однако, также ясно, что этот “белый шум” является очень тяжелой помехой. Если уметь бороться с такой помехой, то с остальными должно быть проще.

В общем случае, на входе некоторого блока с передаточной функцией W(p):

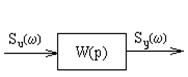S_y(w)=|W(j w)|² * S_u(w)

В частном случае для “белого шума” с единой спектральной плоскостью:

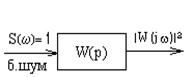“Белый шум” прошедший через линейную систему называют “розовым шумом”.

Фильтр Винера (Норберт Винер).

Задача - построить устройство-фильтр, максимально возможно подавляющее помеху с известной спектральной плоскостью, предполагая что полезный сигнал также случайный сигнал, с известной спектральной плоскостью.

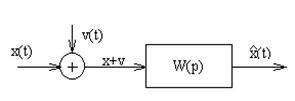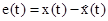- ошибка фильтрации

Задача - определить W(p), чтобы D(e) -> min, при известных характеристиках x(t) и v(t).

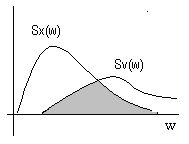
Обычно известны или корреляционные функции, или спектральные плоскости.

Также оказывается необходимым знать взаимную корреляционную функцию или взаимную спектральную плотность полезного сигнала и шума. Важным является стационарность случайных сигналов, отсутствие дополнительной информации о сигналах при наличии которых фильтрацию можно улучшить и известные статистические характеристики сигналов

Более общей является постановка задачи по Калману. Эта постановка более общая по причинам:

1. Процессы могут быть нестационарными.

2. Уравнения объекта могут быть нестационарные, т.е. вообще не описываться передаточной функцией.

3. Все процессы могут быть векторными.