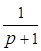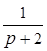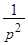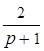Для типовых входных сигналов лишь конечное число производных не равно нулю

Например: ;

;

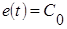Выясним, от чего зависит .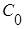

;

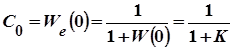Есть другой способ уменьшения 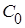и ,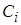

если в разомкнутой системе имеется несколько интеграторов:

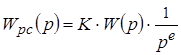, при этом 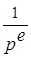“могут быть в любом месте”.

,

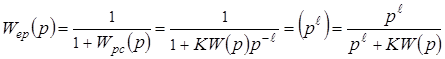при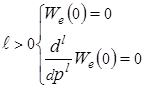

т.е. , ,..., .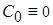

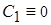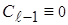При наличии 1 интегратора в системе 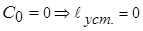, при;

Если 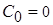из-за наличия интегратора, то система обладает астатизмом.

Если , то система обладает астатизмом n-ного порядка.

Порядок астатизма: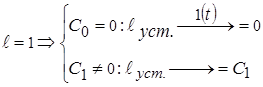

; ; ;

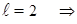
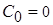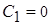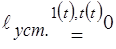Добавление в состав регулятора нескольких интегральных звеньев позволяет повысить порядок астатизма, тем самым обеспечить нулевую установочную ошибку для достаточно сложного вида входного воздействия.

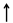Речь идет о статической точности. Если первая функция замкнутой системы имеет корень хар. уравнения ближайший к нулю 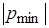: Im

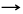
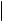
Re

то ряд (#) будет сходиться лишь внутри круга меньшего радиуса. min

Величине 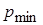соответствует время .

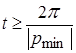При возрастании общего К уменьшаются все коэффициенты ошибок, однако, необходимо помнить про запас устойчивости по амплитуде.

Убедимся, однако, что и добавление интегратора может сделать систему неустойчивой.

Пример

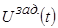
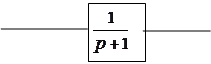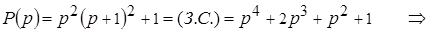неустойчивая система, так как a₃ = 0 (не выполняется необходимое условие устойчивости).

Из этого примерка видно, что возможности повышения астатизма ограничены.

Чтобы повысить порядок астатизма и не потерять устойчивость вместо интегратора можно подключать так называемые изодронные звенья.

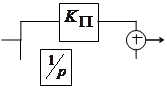Выбором 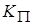можно обеспечить порядок астатизма и сохранить устойчивость.