Точность по возмущающему воздействию

Лекция 15

Точность по возмущенному воздействию, коэффициенты ошибок по возмущению определяются аналогично.

W1

W2

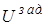е f

;

;

;

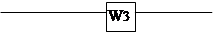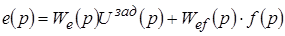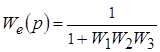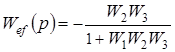Замечание: Система, обладающая астатизмом по управляющему воздействию, может не быть астатической по возмущающему.

Пример:

f

е

;

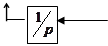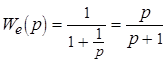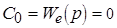- астатизм по заданному воздействию.

;

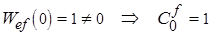- нет астатизма по возмущению.

Для обеспечения астатизма интегратор должен быть включен до места приложения воздействия.

Обеспечение динамической точности - задача гораздо более сложная, так как требует изучения всего переходного процесса.

Принцип инвариантности. Принцип комбинированного управления c

обратной связью по отклонению и по возмущенному воздействию.

Идея метода: помимо общего замыкания системы обратной связью и построения регулятора, дополнительно вводится в систему ветвь прохождения нежелательного сигнала, и коэффициент передачи в этой ветви подбирается так, чтобы повысить точность.

Попытаемся добавить в стандартную структуру системы дополнительную первичную функцию 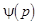так, чтобы сигнал ошибки вообще не зависел от задающего воздействия.

U (p)

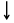
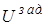
е

;

; (*)

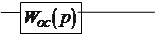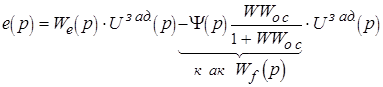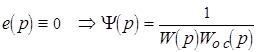Можем обеспечить инвариантность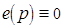

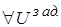
2) Требуется выяснить, как изменяется устойчивость при введении 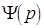. 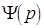не влияет на устойчивость.

!

Однако, и это основной недостаток принципа инвариантности, из формулы (*) очевидно, что,

либо: физически не реализуемо 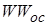, а 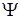- реализуемо.

либо: наоборот.

Поэтому, в точности инвариантность реализовать невозможно, однако, взяв несколько первых членов разложения в ряд Тейлора:

;

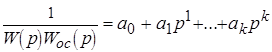Можно добиться сколь угодно большой точности заменой этих дифференцирующих звеньев на реальные дифференцирующие звенья.

Таким образом введением производных от задающего воздействия можно с наперед заданной точностью решить задачу инвариантности.