Анализ и синтез САР

порядок анализа и синтеза автоматических систем зависит от условий поставленной задачи и состояния САУ на момент исследования.

Если САУ уже спроектирована и исследователю необходимо теоретически проверить работоспособность с заданными показателями, то весь расчет будет носить проверочный характер. Если САУ в процессе

В практической работе при исследовании систем автоматического регулирования приходится иметь дело с двумя задачами.

В одних случаях при заданной системе автоматического регулирования требуется найти переходные процессы, в ней в ней возникающие.исследовать работу системы, найти процессы, в ней возникающие. Это задача анализа САР. В задачу анализа, таким образом, входят исследование динамического и статического режимов работы САР, исследование устойчивости системы.

В других случаях при заданных объекте управления и требования к системе управления этим объектом, надо спроектировать такую САР, которая удовлетворяла бы поставленным требованиям. Это задача синтеза САР.

Обе задачи имеют много общего и в значительной степени связаны друг с другом. К настоящему времени задачи анализа и синтеза линейных САР в значительной степени решены. Что же касается решения этих задач для нелинейных САР, то оно пока далеко от завершения.

Большая часть этого учебного пособия будет посвящена задаче анализа систем автоматического регулирования, создания и использования инструментария этого анализа.

В практике автоматического регулирования часто возникает задача сравнивания нескольких САР и выбора из них лучшей в том или ином смысле. Естественной представляется идея подать на все эти системы одинаковые пробные (тестовые) сигналы и по реакции на приложенные воздействия судить о качестве регулирования в каждой из них.

В теории автоматического регулирования применяются разнообразные тестовые сигналы. Нам понадобятся в дальнейшем три из них.

а) Единичный скачок (рис. II.27)

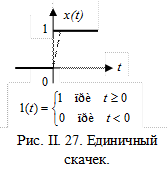Понятно, что это сигнал является известной идеализацией реального скачка, т.к. для того, чтобы провести изменения сигнала от нулевого до любого значения мгновенно, устройство, производящее это изменение, должно обладать бесконечно большим коэффициентом усиления. Реальное устройство будет изменять сигнал законченное время по некоторой зависимости, изображенной на рис. II.17 пунктирной линией, причем наклон этой линии зависит от коэффициента усиления устройства. Тем не менее, в дальнейшем мы будем употреблять идеализированное выражение этого сигнала.

б) Единичный импульс [дельта-функция Дирака d(t) ] (рис. II.28)

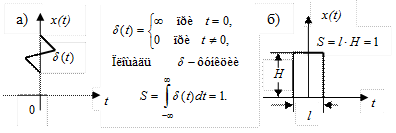
Рис. II.28 Единичный скачек.

Под единичным импульсом (d - функцией Дирака) понимают импульс бесконечно малой длительности бесконечно большой амплитуды с площадью S = 1 (рис. II.28 а). Значок 7- условное обозначение d - функции. Понятно, что, как и в предыдущем случае, речь идет о некоторой идеализации, понять которую можно, обратившись к рис. II. 28 б. Пусть имеется импульс длительности l и амплитуды Н, площадь которого 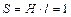. Будем не изменяя площади, уменьшать длительность импульса l, увеличивая тем самым его амплитуду Н. В пределе как раз и получится d - функция.

в) Гармоничный сигнал .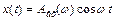

При анализе систем автоматического регулирования их можно исследовать во времени и частотной областях.

8. Поведение САР во временной области.

Различают две характеристики, описывающие поведение САР во временной области – переходная функция (характеристика) САР и импульсная переходная (весовая) функция системы.

8.1. Переходная характеристика САР.

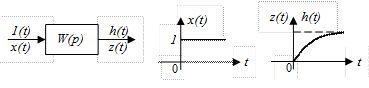
Рис. II. 29. Переходная характеристика САР.

Под переходной характеристикой САР h(H) понимают ее (САР) реакцию на единичный скачок 1(t) (рис. II. 29).

На рис. II.29 а представлена САР с известной передаточной функцией W(p), на вход которой подается единичный скачок х(t) = 1(t), приведенный и на рис. II.29 б. На выходе САР, появляется сигнал z(t) зависящий от ее конкретного вида, который при единичном входном скачке, есть переходная характеристика САР, т.е. z(t) = h(t) (рис. II.29 в).

Характеристику h(t) через известную передаточную функцию системы W(р) можно найти следующим образом.

Известно, что изображения выходной и входной величины связаны соотношениями

В нашем случае изображение выходного сигнала 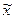, являющегося единичным сигналом, согласно [ ] определяется следующим образом

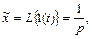
поэтому

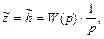
а, значит,

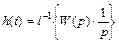(II.8.1)

т.е. переходная характеристика САР определяется как обратное преобразование Лапласа от произведения передаточной функции САР на изображение единичного скачка. Переходная характеристика является очень мощным инструментом анализа системы, позволяющая оценить многие важные показатели работы САР – устойчивость, быстродействие, перерегулирование, точность и т.п. (см. главы V и VI).

8.2. Импульсная переходная (весовая) функция системы.

Весовая функция САР W(t) есть ее (САР) реакция на входной единичный импульс d(t) (рис. II.30).

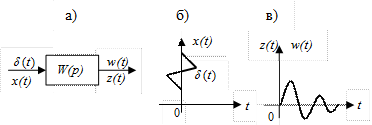
Рис. II. 30. Весовая функция САР.

На вход САР с известной передаточной функцией W(p) (рис. II.30а) подается d - функция Дирака 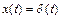(см. рис. II 30б). В зависимости от САР на ее входе появляется определенный выходной сигнал 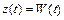, являющейся по определению весовой функцией. Найти весовую функцию САР можно аналогично вышеизложенному

Согласно [ ] изображение d - функции определяется выражением

,

тогда

.

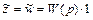Отсюда

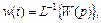(II.8.2)

т.е. весовая функция ЧАР может быть определена как обратное преобразование Лапласа от передаточной функции САР.

Сравнивая (II.8.1) и (II.8.2) нетрудно понять, что

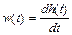(II.8.3)

Зная весовую функцию САР w(t) для произвольного входного сигнала x(t) можно с помощью интеграла Дюамеля найти выходной сигнал системы z(t)

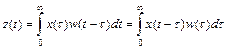. (II. 8.4)