Критерий Гурвица. Определитель Гурвица составляется по следующему правилу: главная диагональ определителя размером n x n последовательно заполняется коэффициентами

Определитель Гурвица составляется по следующему правилу: главная диагональ определителя размером n x n последовательно заполняется коэффициентами характеристического уравнения, начиная с коэффициента при (n-1) производной до свободного члена. Столбцы вверх от главной диагонали дополняют последовательно коэффициентами с возрастающими индексами, а столбцы вниз – коэффициентами с убывающими индексами. Места, которые должны быть заняты коэффициентами с индексом выше а_n и ниже а₀, заполняют нулями.

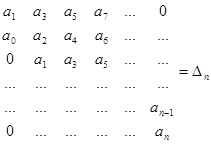
Формулировка:

Для того, чтобы характеристическое уравнение системы имело все корни с отрицательной вещественной частью необходимо, чтобы главный определитель Гурвица и все его диагональные миноры D_n-1, D_n-1, …, D₂, D₁ имели один знак с коэффициентом при старшей производной.

Пример:

1. Система 1-го порядка.

- критерий Гурвица выражается в систему двух неравенств

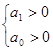
2. Система 2-го порядка.

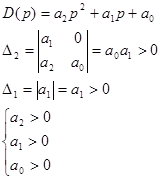
3. Система 3-го порядка.

Достоинства критерия:

1. Сравнительная простота.

Недостатки:

1. Громоздкость вычислений при n>4.

2. Алгебраические критерии дают ответ на вопрос, устойчива система или нет, но ничего не говорят о том, что надо сделать, чтобы система стала устойчивой.

С инженерной точки зрения более применим частотный критерий устойчивости.