Критерии – это признаки, по которым можно судить об устойчивости системы без решения дифференциального уравнения динамики системы и без вычисления корней.
Все критерии делятся на алгебраические, которые основаны на анализе коэффициентов характеристического уравнения, и частотные, которые основаны на анализе частотных характеристик системы.
1. Алгебраические критерии устойчивости.
1.1. Критерий Стодолы (простейший алгебраический критерий).
Простейшим необходимым, но недостаточным критерием устойчивости является требование того, чтобы все коэффициенты характеристического уравнения имели одинаковый знак.
Докажем это. Пусть имеем устойчивую систему с характеристическим уравнением:
 (1)
(1)
В устойчивой системе все корни имеют отрицательную вещественную часть:
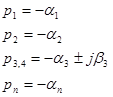 где a и b - неотрицательные числа.
где a и b - неотрицательные числа.
Запишем выражение (1) через корни:
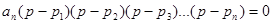
Подставим значения корней:
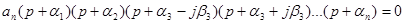
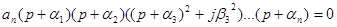
Раскроем скобки и приведем к виду выражения (1). Перемножая или складывая положительные числа нельзя получить отрицательные, то есть все коэффициенты будут положительные или все отрицательные (в зависимости от аn).
Для систем 1-го и 2-го порядков критерий является необходимым и достаточным. Для систем более высокого порядка этот критерий является необходимым, но не достаточным. Если хоты бы один коэффициент характеристического уравнения имеет знак отличный от знаков других коэффициентов, то можно сразу сказать, что система неустойчива и никаких дополнительных исследований не потребуется проводить.
Но положительность всех коэффициентов не гарантирует устойчивости. При некотором соотношении корней с положительной вещественной частью можно тоже получить все коэффициенты одного знака. Здесь требуются дополнительные исследования. Были разработаны другие алгебраические критерии, которые являются как необходимыми, так и достаточными. Наибольшее распространение получили критерий Рауса(E.I. Routh 1877г.) и критерий Гурвица (A.Hurwitz 1895г.).
Оба критерия основаны на построении определителей из коэффициентов характеристического уравнения. В результате они приводят к одной и той же системе неравенств.
 2014-02-02
2014-02-02 578
578








