Частотная характеристика

Пусть входная последовательность x(n) = e^jwn, -¥ < n < ¥ поступает на вход ЛПП с импульсной характеристикой h(n). Тогда выходная последовательность

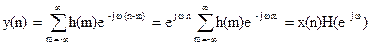
Т.о. отклик ЛПП совпадает с входной последовательностью с точностью до комплексного множителя H(e^jw), который выражается через импульсную характеристику следующим образом:

Это частотная характеристика системы или коэффициент передачи ЛПП-системы для каждого значения w.

Пример. Вычислить ч.х. ЛПП-системы с импульсной характеристикой:

h(n) = aⁿU_-1(n) (| a | < 1).

Ч.х. имеет вид:

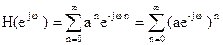(2)

т.к ½a½<1, то сумма геометрической прогрессии (2) будет равна

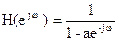
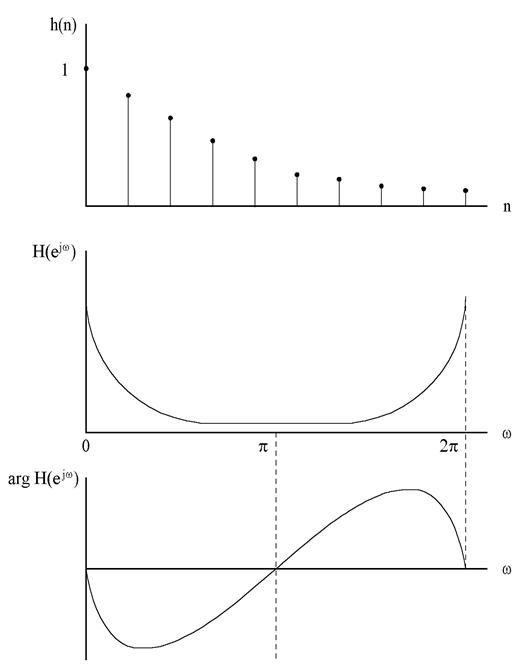
Свойства ч.х.

1) Периодическая функция w с периодом 2p.

2) Для действительных h(n), модуль H(e^jw) симетричен, а фаза H(e^jw) антисимметричен на интервале 0£w£2p. Поэтому для действительных h(n) ч.х. выделяют на сокращенном интревале частот 0£w£p.