Лекция №4
Контрольные вопросы
1. Зависит ли соотношение (1) от формы замкнутой поверхности?
2. Почему внутри металла электростатическое поле отсутствует?
3. Почему на металлической поверхности тела вектор напряжённости электростатического поля нормален к поверхности металла?
4. Произведите вывод соотношения (3).
5. Произведите вывод соотношения (4).
Градиент электростатического поля. Теорема Гаусса в дифференциальной форме. Уравнения Лапласа и Пуассона.
1. Производная от скалярной функции по направлению. Градиент скалярной функции.
2. Дивергенция функции. Теорема Гаусса в дифференциальной форме.
3. Уравнения Лапласа и Пуассона.
4. Единственность решений уравнений Лапласа и Пуассона, граничные условия. Задачи Дирихле, Неймана и смешанные.
 Краткое содержание лекции
Краткое содержание лекции
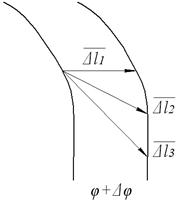
Для определения производной от функции потенциала по направлению l, а от направления зависит величина производной (рис.1), выполняются следующие преобразования:
Рис. 1
Здесь 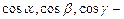 косинусы углов между осями координат
косинусы углов между осями координат 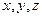 и единичным вектором
и единичным вектором 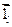 .
.
Результат преобразований (1) можно представить как производные двух векторов:
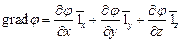 и
и 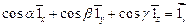
Таким образом, производную по направлению 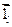 можно записать так:
можно записать так:
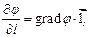
При этом 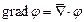 , где
, где 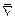 – оператор Гамильтона:
– оператор Гамильтона:
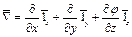 .
.
Очевидно, что 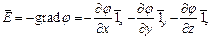 .
.
Здесь градиент функции записан в декартовой системе координат. Теорему Гаусса, записанную в интегральной форме, преобразуют следующим образом:
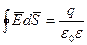
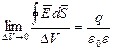
Если ΔV устремляется к нулю, то в итоге получаем:
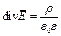
или
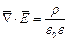
| (2) |
В декартовой (прямоугольной) системе координат:
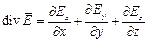
Поскольку 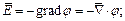 а также
а также 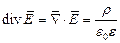 , то
, то 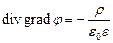 , или
, или
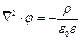
| (3) |
Уравнение (3) называется уравнением Пуассона.
Если свободный электрический заряд отсутствует, то есть 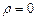 , то получается уравнение Лапласа:
, то получается уравнение Лапласа:
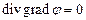
или
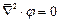
В декартовой системе координат уравнения Лапласа, Пуассона записываются так:
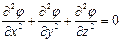
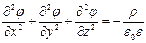
| (4) |
Уравнения (4) являются уравнениями в частных производных, и решение в аналитической форме для них получается в весьма ограниченном круге областей решения, когда эти уравнения можно свести к уравнениям от одной переменной, то есть к обыкновенным дифференциальным уравнениям.
Уравнения (4) имеют единственное решение. Для решения (4) необходимо задать граничные условия. Граничные условия бывают трёх видов:
· на границе задаётся функция φ (задача Дирихле);
· на границе задаётся производная φ нормальная к границе 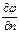 (задача Неймана);
(задача Неймана);
· задаётся и функция, и её производная, φ и 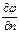 (смешанная задача).
(смешанная задача).
В зависимости от геометрии области, в которой производится решение уравнения Лапласа, используется та или иная система координат.
В общем случае уравнения Лапласа и Пуассона решаются численными методами.
Картину поля, то есть эквипотенциальные и силовые линии, можно построить графически. Для этого необходимо придерживаться трёх правил:
1. Силовые линии должны быть нормальны к границе области, которая представляет собой металлическое тело.
2. Эквипотенциальные и силовые линии должны пересекаться под прямым углом.
3. Фигуры, которые получаются в результате пересечения эквипотенциальных и силовых линий, должны быть подобными.
После построения картины поля можно найти приближённые значения напряжённости и индукции электростатического поля.
Уравнения Лапласа и Пуассона решаются в определенной области пространства, которое ограничено границами.
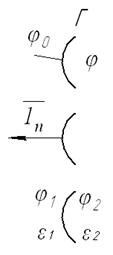
1) Задача Дирихле
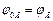
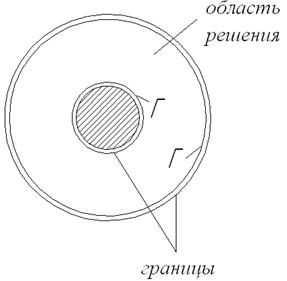
2) Задача Неймана
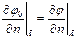
3) Смешанная задача
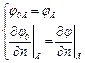
Далее рассматриваются граничные условия решения уравнений Лапласа, Пуассона. Рассмотрим преломление вектора индукции на границе двух сред.
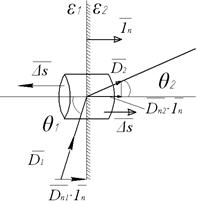
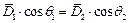
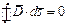
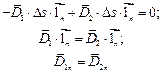
Следовательно, на границе двух сред с различными диэлектрическими проницаемостями ε1, ε2 нормальные составляющие вектора индукции равны между собой.
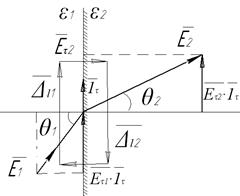 Рассмотрим преломление вектора напряженности на границе двух сред.
Рассмотрим преломление вектора напряженности на границе двух сред.
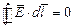
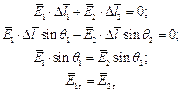
Касательные составляющие векторов напряженности равны между собой.
Так как 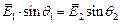 ,
, 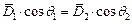 и
и 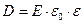 , то запишем:
, то запишем:
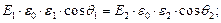
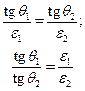
Это является условием преломления силовых линий векторов 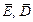 .
.
Выделим у границы двух сред с относительной диэлектрической проницаемостью небольшой цилиндрический объем круглого сечения. Согласно теореме Гаусса,
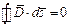
| (5) |
так как внутри цилиндра свободных зарядов нет.
Поскольку цилиндр мал, по его объему вектор индукции постоянен. Интеграл (5) заменяется приближенным соотношением:
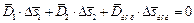 ,
,
где  – вектор индукции на боковой поверхности;
– вектор индукции на боковой поверхности; 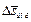 – вектор боковой поверхности.
– вектор боковой поверхности.
С точки зрения макроскопической теории поля, существуют только объемные заряды. Однако, в том случае, когда электрические заряды занимают тонкий поверхностный слой, толщина которого много меньше расстояния до точки наблюдения, можно считать, что все заряды расположены в бесконечно тонком поверхностном слое. Это касается металлических тел в первую очередь. Так как при прохождении через заряженную поверхность вектор 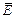 меняется скачком,
меняется скачком,
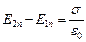 , ,
| (5) |
что можно показать с помощью теоремы Гаусса.
Пусть некоторый вектор 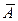 всюду непрерывен и конечен и всюду удовлетворяет уравнению
всюду непрерывен и конечен и всюду удовлетворяет уравнению
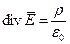 , ,
| (6) |
где ρ – плотность некоторого заряда q.
Рассмотрим некоторый заряженный слой конечной толщины Δ l, внутри которого вектор 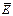 является непрерывным (рис. 1).
является непрерывным (рис. 1).
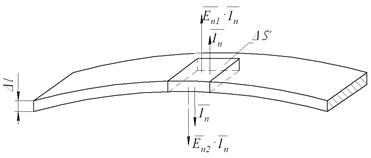
Если, оставляя неизменным заряд слоя, уменьшать его толщину Δ l до бесконечно малой величины, то непрерывность вектора 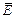 нарушается.
нарушается.
При рассмотрении цилиндрического участка заряженного слоя площадью 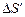 , умножая (5) на dV и интегрируя по объему, получаем:
, умножая (5) на dV и интегрируя по объему, получаем:
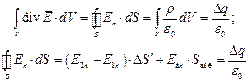 , ,
|
где Ебn – нормальная составляющая напряженности боковой поверхности;
Sбок – боковая поверхность.
Если 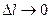 , то
, то 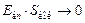 . В итоге получается:
. В итоге получается:
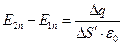 или
или 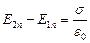
Величина 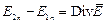 – поверхностная дивергенция. Надо обратить внимание, что операция
– поверхностная дивергенция. Надо обратить внимание, что операция 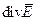 – это дифференцирование функции
– это дифференцирование функции 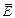 , а операция
, а операция 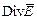 – это разность функций. Поэтому если ρ является функцией от координат, то σ является производной этой функции.
– это разность функций. Поэтому если ρ является функцией от координат, то σ является производной этой функции.
Пример. Имеется шар радиусом а, внутри которого имеется распределенный заряд плотностью ρ. Найти напряженность и потенциал поля как функции R.
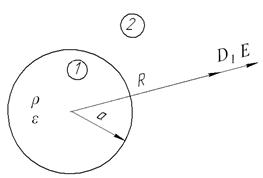
Рис. 2
Для области 1 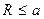 уравнение Пуассона:
уравнение Пуассона:
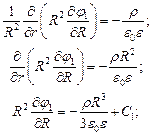
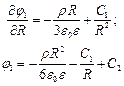
Для области 2 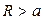 уравнение Лапласа:
уравнение Лапласа:
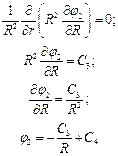
Пусть при 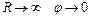 , тогда
, тогда 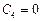 .
.
Условие на границе при 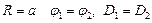
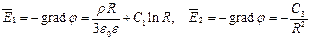
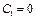 , так как в центре шара R = 0, и
, так как в центре шара R = 0, и 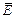 не может равняться бесконечности.
не может равняться бесконечности.
Тогда 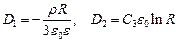
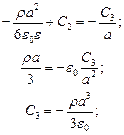

Найденные постоянные подставляем в уравнения:
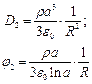
 2014-02-02
2014-02-02 468
468








