Предисловие
Луганск 2013
Электротехники.
Кривошеев Е.И.
Яковенко В.В.
Имени ВЛАДИМИРА ДАЛЯ
ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
И СПОРТА УКРАИНЫ
Электромагнитное поле.
Электротехники.
Теоретические основы
Кривошеев Е.И.
Яковенко В.В.
Имени ВЛАДИМИРА ДАЛЯ
ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
И СПОРТА УКРАИНЫ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ, МОЛОДЕЖИ
Рекомендации программисту.
Как виртуальные должны быть описаны методы, которые выполняют во всех классах иерархии одну и ту же функцию, но, возможно, разными способами. Пусть, например, все объекты иерархии должны уметь выводить информацию о себе. Поскольку эта информация хранится в различных полях производных классов, функцию вывода нельзя реализовать в базовом классе. Естественно назвать ее во всех классах одинаково и объявить как виртуальную с тем, чтобы ее можно было вызывать в зависимости от фактического типа объекта, с которым работают через базовый класс.
Обычные (не виртуальные) методы переопределять в производных классах не рекомендуется, поскольку производные классы должны наследовать свойства своих базовых классов, а спецификатор new, с помощью которого переопределяется обычный метод, " разрывает " отношение наследования на уровне метода. Иными словами, невиртуальный метод должен быть инвариантен относительно специализации, то есть должен сохранять свойства, унаследованные из базового класса независимо от того, как конкретизируется (специализируется) производный класс.
|
|
|
Специализация производного класса достигается добавлением новых методов и переопределением существующих виртуальных методов.
Луганск 2013
МИНИСТЕРСТВО ОБРАЗОВАНИЯ, МОЛОДЕЖИ
УДК 621.301
Яковенко В.В., Кривошеев Е.И. Теоретические основы электротехники.Электромагнитное поле: Учебное пособие. – Луганск: ВУНУ, 2013. – 126 с.
В учебном пособии приводятся сведения об электромагнитном поле (электродинамика). При написании пособия ставилась цель удовлетворить запросы к теоретическим основам электротехники со стороны студентов электротехнических специальностей. Авторы стремились к элементарному изложению математических моделей электромагнитных полей, для понимания которых требуются минимальные знания математического анализа и векторного исчисления.
Пособие содержит разделы электростатического поля, поля постоянного тока, магнитостатического поля, электромагнитного поля в проводящей среде и в диэлектрике. Материал в пособии изложен в виде отдельных лекций.
Пособие содержит некоторые сведения из электродинамики, которые не входят в традиционные учебники.
|
|
|
Основные математические понятия, используемые в электродинамике.
План лекции:
1. Пространственные системы координат.
2. Основные понятия векторного исчисления.
3. Векторное поле и его характеристики..
Краткое содержание лекции
Пространственные системы координат
В электродинамике используются в основном три вида пространственных систем координат: прямолинейная (или декартова система, по имени французского математика Р.Декарта), цилиндрическая и сферическая.
В декартовой системе координат (рис. 1) координатными линиями являются прямые, а координатными поверхностями – плоскости. Элементы длины по координатным линиям соответственно равны:
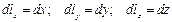
Элементы поверхности по координатным плоскостям образуются так: в координатной плоскости XOY: 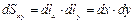 ; в плоскости XOZ:
; в плоскости XOZ: 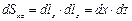 ; в плоскости YOZ:
; в плоскости YOZ: 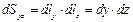 .
.
Элемент объема будет равен:
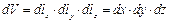
Элементарные единичные векторы или орты, обозначаемые в математике 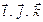 , будут в электродинамике обозначаться
, будут в электродинамике обозначаться 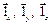 .
.
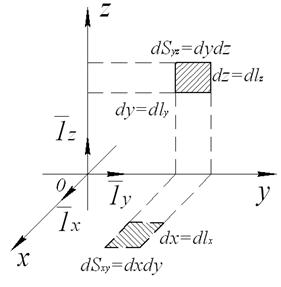
Рис. 1. Прямоугольная (Декартова) система координат.
В цилиндрической системе координат (рис. 2) координатными линиями будут прямые, параллельные оси z, лучи параллельные оси r, и окружности, лежащие на цилиндрической поверхности, а координатные поверхности представляют собой плоскость при z = cоnst и цилиндрическую поверхность при r = const.
Элементы длины, площадей и объема равны:
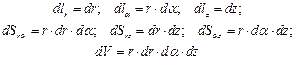
Элементарные единичные векторы (орты) – 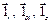 . Орт
. Орт 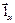 направлен по касательной к координатной линии – окружности, лежащей на цилиндрической поверхности. Угол α изменяется от 0 до 2π. Радиус r и координата z изменяется от нуля до бесконечности.
направлен по касательной к координатной линии – окружности, лежащей на цилиндрической поверхности. Угол α изменяется от 0 до 2π. Радиус r и координата z изменяется от нуля до бесконечности.
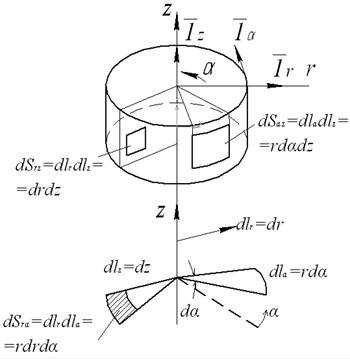
Рис. 2. Цилиндрическая система координат.
В сферической системе координат (рис. 3) координатные линии представляют собой:
– луч – координата r, изменяющаяся от нуля в центре системы координат О до бесконечности;
– полуокружность r = const, α = const, образующаяся при движении конца радиуса r, когда угловая координата θ изменяется от 0 до π;
– окружность, образующаяся при движении конца радиуса r, когда угловая координата α изменяется от 0 до 2π.
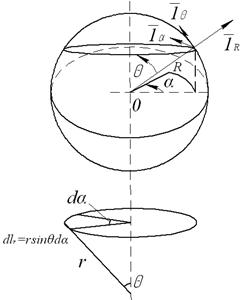
Рис. 3. Сферическая система координат.
Координатные поверхности имеют вид:
– при α = const изменяющиеся координаты r и θ образуют полуплоскость;
– при θ = const изменяющиеся координаты r и α образуют коническую поверхность;
– при r = const изменяющиеся координаты θ и α образуют сферу.
Единичные векторы 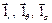 взаимно перпендикулярны, а орты
взаимно перпендикулярны, а орты 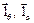 касательны к полуокружности r = const, α = const и к окружности r = const, θ = const.
касательны к полуокружности r = const, α = const и к окружности r = const, θ = const.
Элементы длин, площадей и объема равны:
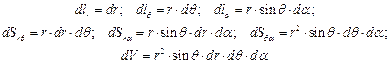
Основные понятия векторного исчисления
Вектором называется величина, имеющая численный размер и определенное направление в пространстве. Векторы описывают такие физические величины как силы, скорости, ускорения, напряженность электрического, магнитного и гравитационного полей, поэтому их можно назвать физическими векторами.
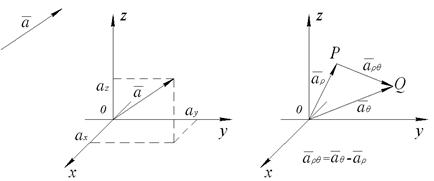
Рис. 4. Векторы в декартовой системе координат
На рис. 4 показаны векторы в прямоугольной системе координат. Радиус-вектор 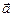 может быть представлен как сумма векторов проекций:
может быть представлен как сумма векторов проекций:
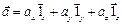
Вектору 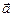 соответствует тройка чисел
соответствует тройка чисел 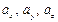 – тройка его координат. Модуль вектора
– тройка его координат. Модуль вектора 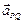 или расстояние между точками P и Q рассчитывается по формуле:
или расстояние между точками P и Q рассчитывается по формуле:
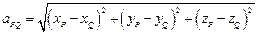
Вектор 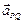 является разницей между векторами
является разницей между векторами 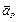 и
и 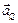 , то есть:
, то есть:
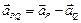
Сложение векторов производится геометрически:
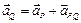 ,
,
а умножение двух векторов может быть скалярным и векторным.
Скалярное произведение векторов 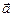 и
и 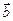 есть произведение модулей векторов на косинус угла между ними:
есть произведение модулей векторов на косинус угла между ними:
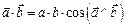
и является скалярной величиной.
Для коллинеарных векторов, то есть векторов, параллельных одной и той же прямой, скалярное произведение максимальное, а для перпендикулярных – равно нулю.
Если векторы представлены в виде суммы составляющих, то есть:
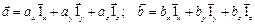 ,
,
то скалярное произведение векторов будет равно:
|
|
|
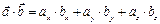
Векторное произведение двух векторов (рис. 5) равно произведению их модулей на синус угла между ними:
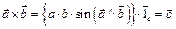
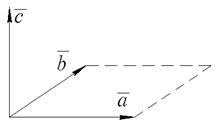
Рис. 5. Векторное произведение двух векторов
Если векторы выражаются в проекциях, то векторное произведение равно:
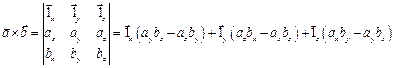
Вектор 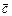 перпендикулярен к плоскости, в которой лежат векторы
перпендикулярен к плоскости, в которой лежат векторы 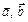 , и направленный от плоскости, если вектор
, и направленный от плоскости, если вектор 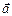 может быть повернут к вектору
может быть повернут к вектору  против часовой стрелки.
против часовой стрелки.
При различных математических операциях, отображающих реальные явления природы, удобно изучать векторы путем их проекций на какие-либо выбранные направления. Наиболее общими способами проекций являются проекции вектора на координатные оси в какой-либо системе координат:
– в декартовой: 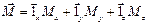 ;
;
– в цилиндрической: 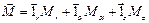 ;
;
– в сферической: 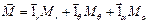
Проекции Мα и Мθ в цилиндрической и сферической системах координат образуются путем проекции вектора 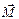 на касательную к координатной линии α или θ в точке приложения вектора.
на касательную к координатной линии α или θ в точке приложения вектора.
Проекции вектора на нормальное (перпендикулярное) и тангенциальное (касательное) направления к какой-либо кривой (рис. 6, а):
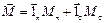 .
.
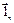 и
и 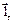 есть орты нормали и касательной к кривой.
есть орты нормали и касательной к кривой.
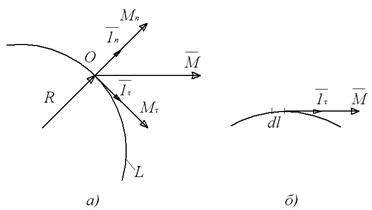
Рис. 6. а) Разложение вектора 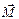 в точке О на две проекции
в точке О на две проекции
относительно кривой L (нормаль 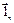 имеет положительное
имеет положительное
направление, а 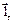 – отрицательное); б) силовая линия вектора
– отрицательное); б) силовая линия вектора
Если взять линию L, для которой вектор 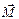 всегда во всех точках касателен, то такая линия называется векторной или силовой линией, или линией тока (рис.6, б). Вводится понятие ориентированного элемента длины:
всегда во всех точках касателен, то такая линия называется векторной или силовой линией, или линией тока (рис.6, б). Вводится понятие ориентированного элемента длины:
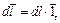 ,
,
удобного для ряда математических преобразований в векторном анализе.
Расширением понятия нормальной и тангенциальной проекции вектора на кривую является введение нормали и касательной к произвольной поверхности S в произвольной ее точке (рис. 7, а).
Весьма важным в векторном исчислении понятием является введение ориентированных элементарных площадок (рис. 7, б)
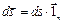 ,
,
представляющих собой обычный элемент поверхности с нормалью к поверхности.
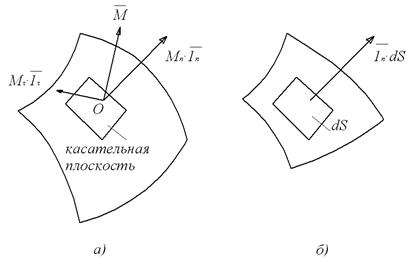
Рис. 7. а) Нормальная и тангенциальная проекции вектора 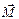
к поверхности S; б) ориентированная элементарная площадка
Легко видеть, что:
|
|
|
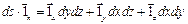 ,
,
где 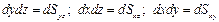 есть элементарные площадки на координатных плоскостях.
есть элементарные площадки на координатных плоскостях.
Векторное поле и его характеристики
Векторным полем называется часть пространства, в котором имеется группа векторов (рис. 8), величина и направление которых отражает физическую суть изучаемого явления.
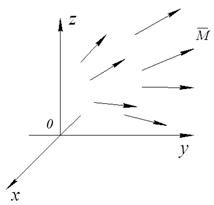
Рис. 8. Поле векторных величин (векторное поле).
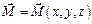 – вектор, величина и направление которого
– вектор, величина и направление которого
различно в различных точках поля.
Для применения в электродинамике группа векторов, составляющих векторное поле, записывается в виде одного вектора 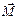 , представленного в проекциях, где каждая проекция в общем случае является функцией трех координат:
, представленного в проекциях, где каждая проекция в общем случае является функцией трех координат:
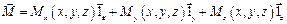
Таким образом происходит описание векторного поля в пространстве как в декартовой, так и в других системах координат. В электродинамике проекции вектора 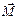 могут быть также функциями времени.
могут быть также функциями времени.
Выражение векторных операций в различных системах координат
1) Декартова система координат
Координаты 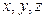
Орты 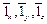
Коэффициенты Ляме 1, 1, 1
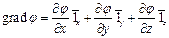
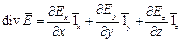
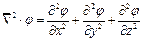
2) Цилиндрическая система координат.
Координаты 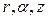
Орты 
Коэффициенты Ляме 1, 1, 1
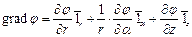
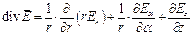 ;
;
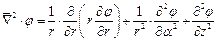
3) Сферическая система координат.
Координаты 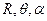
Орты 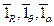
Коэффициенты Ляме 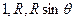
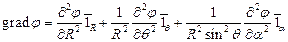
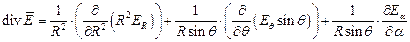 ;
;
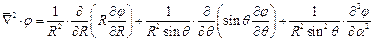
Контрольные вопросы:
1. Какие координатные линии в сферической системе координат?
2. Чему равно скалярное произведение векторов 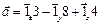 и
и 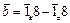 ?
?
3. Чему равно векторное произведение векторов 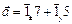 и
и 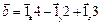 ?
?
 2014-02-02
2014-02-02 945
945







