План лекции. 1. Запишите операцию градиент в цилиндрической и сферической системах координат

Лекция №5

Контрольные вопросы

1. Запишите операцию градиент в цилиндрической и сферической системах координат.

2. Что такое оператор Гамильтона?

3. Запишите с помощью оператора Гамильтона операции градиента, дивергенции, оператора Лапласа.

4. Зачем необходимы граничные условия, и какого вида они бывают?

5. Какие системы координат Вы знаете? Что такое коэффициенты Ляме?

Емкость. Частичные ёмкости. Потенциальные коэффициенты.

Энергия электростатического поля.

1. Понятие ёмкости, метод расчёта ёмкости.

2. Потенциальные коэффициенты, частичные ёмкости, ёмкости электропроводных линий.

3. Ёмкости плоских, цилиндрических и сферических конденсаторов.

4. Энергия электростатического поля, выражение энергии через величину зарядов.

Краткое содержание лекции

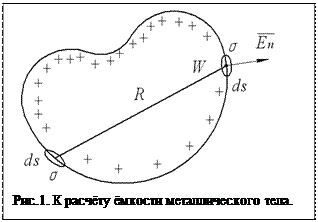Если взять металлическое тело (рис.1) и сообщить ему некоторый заряд, то весь заряд распределится по поверхности тела с плотностью заряда σ. Плотность заряда на поверхности тела будет таковой, что электростатическое поле внутри тела будет отсутствовать, а на поверхности вектор напряжённости поля будет нормален к поверхности металлического тела. Элементарная площадка поверхности металлического тела создаёт на расстоянии R следующий потенциал:

,

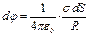а поверхность металлического тела в одной точке поверхности создаёт потенциал, равный:

.

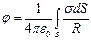Очевидно, что при различных значениях сообщаемого телу заряда распределение заряда по поверхности не изменится, поэтому можно записать: .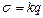

Таким образом, величину интеграла 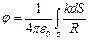можно принять за характеристику формы и размеров металлического тела и обозначить её:

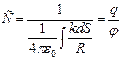
За величину ёмкости принимается величина равная:

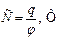
Например, ёмкость шара равна: 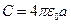(а – радиус шара)

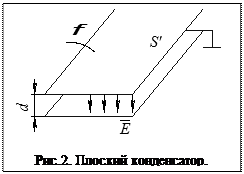Ёмкость плоского

конденсатора

Если потенциал одной пластины равен φ, а второй нулю, то вследствие однородности поля напряжённость между пластинами равна:

.

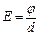Плотность заряда на пластине будет величиной постоянной и равной:

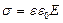
Поэтому на пластине будет заряд: .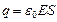

Ёмкость плоского конденсатора определяется формулой

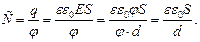
Ёмкость цилиндрического конденсатора

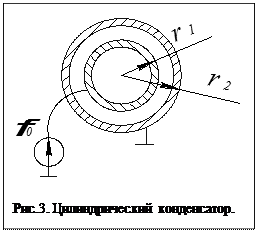Уравнение Лапласа для заданной задачи имеет вид:

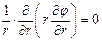
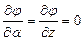
Интегрируя, получаем:

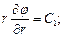
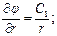
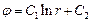
Формула для напряжённости поля имеет вид:

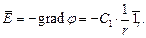
Граничные условия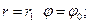: при при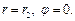

Используя граничные условия, получаем:

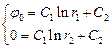
откуда:

,

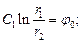
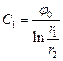Плотность зарядов на внутреннем электроде:

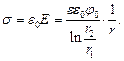
Величина заряда на единицу длины равна:

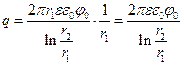
Формула для ёмкости имеет вид:

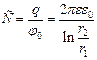
Ёмкость шарового конденсатора

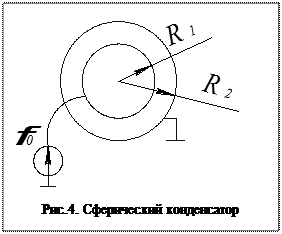Уравнение Лапласа:

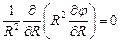
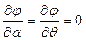
Интегрируя, получаем:

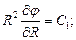
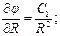
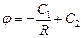
Граничные условия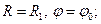: при при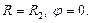

Напряжённость поля: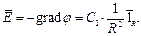

Используя граничные условия, получаем:

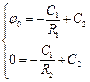
откуда:

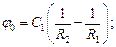
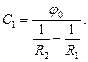
Напряжённость электростатического поля между пластинами:

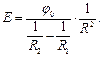
Плотность зарядов на внутреннем электроде:

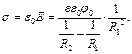
Величина заряда на внутреннем электроде и ёмкость шарового конденсатора равны:

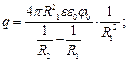
Ёмкость системы металлических тел

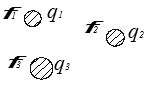Если имеется система заряженных тел, то потенциал каждого тела будет равен:

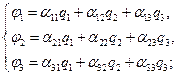(1)

здесь 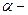потенциальные коэффициенты.

Решая (1) относительно неизвестных 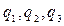, получаем:

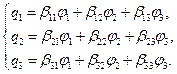
(2)

Коэффициенты β имеют размерность ёмкости и называются емкостными коэффициентами. Коэффициенты вида β_kn принимают отрицательные значения, поэтому система (2) преобразуется к виду:

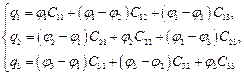
(3)

Ёмкости, входящие в соотношение (3) называются частичными. Приравнивая коэффициенты при одинаковых потенциалах, находим, что:

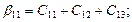
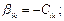
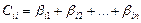
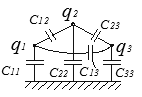
Рис.4. Система трёх проводников и частные ёмкости

Энергия электростатического поля

В некотором объёме величина энергии поля равна:

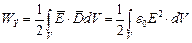
(4)

Интегрирование производится по всему объёму, занимаемого полем. Это не всегда удобно, так как объём может простираться до бесконечности. Преобразуем (4) к виду:

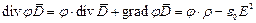
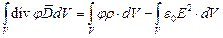
Согласно теореме Остроградского:

.

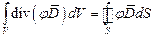При увеличении области до бесконечности 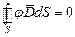, так как φ · D уменьшается как 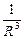, а поверхность S растёт как R².

Поэтому окончательно получаем:

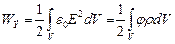
Если имеется несколько точечных зарядов, то их энергия равна:

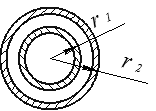Пример 1. Найти емкость цилиндрического конденсатора.

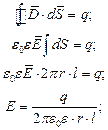
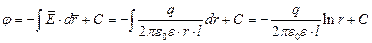
Одно значение потенциала можно взять произвольным. Возьмем 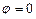при 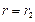. Тогда:

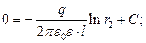
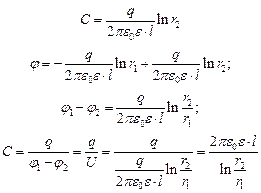
Пример 2.

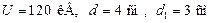
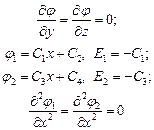
Пр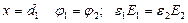и , при ,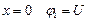

при .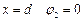

Тогда:

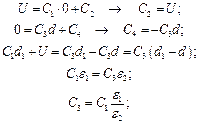
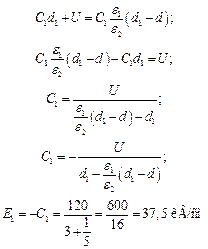
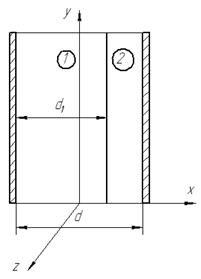
Расстояние между металлическими пластинами (см. рис.) составляет 4 см. К пластинам подведено напряжение 120 кВ. Таким, образом, между пластинами напряженность поля равна 30 кВ/см, то есть равная пробойной для воздуха. Некомпетентным лицом предлагается между пластинами вставить лист стекла (его пробойная напряженность равна 100 кВ/см) для укрепления системы. К чему приведет это предложение?