Поток вектора индукции, теорема Гаусса.
Электростатическое поле в диэлектрике. Электростатическое поле на границе двух сред с различными физическими свойствами.
План лекции:
1. Поток вектора индукции, теорема Гаусса.
2. Поляризация диэлектрика. Диполь. Коэффициент поляризации. Вектор поляризации.
3. Граничные условия на границе металл – диэлектрик.
4. Граничные условия на границе диэлектрик – диэлектрик.
Краткое содержание лекции:
Если некоторую поверхность разбить на N элементарных площадок и поместить в электростатическое поле, то через каждую площадку будет проходить элементарный поток вектора индукции 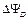 (рис.1):
(рис.1):
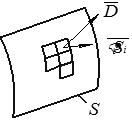
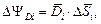
где 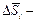 вектор нормальный к площадке и модулем равным величине площадки;
вектор нормальный к площадке и модулем равным величине площадки;
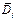 – вектор индукции в i -ой площадке.
– вектор индукции в i -ой площадке.
 Суммарный поток вектора
Суммарный поток вектора 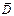 через поверхность S будет равен:
через поверхность S будет равен:
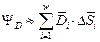
При уменьшении площади элементарных площадок и увеличении их числа в пределе получаем формулу поток вектора индукции:
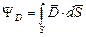
Если заряд q окружить поверхностью произвольной формы, то суммарный поток через замкнутую поверхность будет равен (теорема Гаусса):
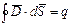 | (1) |
Если внутри заряда нет, то
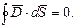
Если замкнутая поверхность охватывает несколько зарядов, то
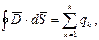
здесь 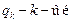 заряд;
заряд; 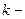 количество зарядов.
количество зарядов.
Диэлектрик представляет собой пространство, заполненное диполями, которые не могут свободно перемещаться, но могут ориентироваться. Диполь имеет момент равный 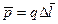 (рис.2).
(рис.2).
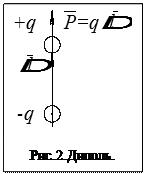 В некотором малом объёме ΔV при отсутствии внешнего электростатического поля сумма моментов диполей равна нулю. При наличии внешнего источника поля диполи ориентируются по полю, и их суммарный момент перестаёт быть равным нулю, а становится равным некоторому суммарному вектору
В некотором малом объёме ΔV при отсутствии внешнего электростатического поля сумма моментов диполей равна нулю. При наличии внешнего источника поля диполи ориентируются по полю, и их суммарный момент перестаёт быть равным нулю, а становится равным некоторому суммарному вектору
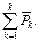
Если этот суммарный вектор отнести к объёму ΔV и последний устремить к нулю, то в результате получается вектор поляризации 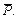
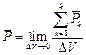 ,
, 
Теперь индукция в диэлектрике будет равной: 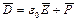
Проделаем следующие операции с модулями векторов:
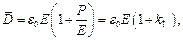
здесь kП – коэффициент поляризованности вещества.
Обозначая, 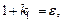 получаем:
получаем:
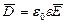 | (2) |
где 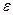 – относительная диэлектрическая проницаемость.
– относительная диэлектрическая проницаемость.
 С учётом (2) теорему Гаусса можно записать так:
С учётом (2) теорему Гаусса можно записать так:
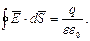
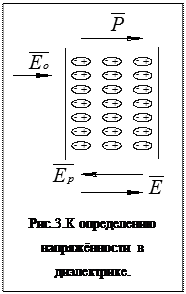
Если рассмотреть полосу диэлектрика в поле вектора 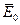 , то можно сделать следующее заключение. Величина индукции в диэлектрике будет равной:
, то можно сделать следующее заключение. Величина индукции в диэлектрике будет равной:
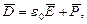
а напряжённость поля 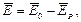
здесь 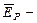 вектор напряжённости поляризации.
вектор напряжённости поляризации.
Поэтому напряжённость поля в диэлектрике будет меньшей, чем вне диэлектрика.
На границе металл – диэлектрик (металл – воздух) вектор напряжённости поля нормален к поверхности металла. Внутри металла вектор напряжённости электрического поля равен нулю, внутри металла электростатического поля нет. На поверхности металла распределён заряд плотностью 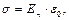 здесь
здесь 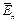 – нормальная составляющая вектора напряженности. Это можно показать с помощью теоремы Гаусса.
– нормальная составляющая вектора напряженности. Это можно показать с помощью теоремы Гаусса.
На границе двух сред с диэлектрическими проницаемостями ε1 и ε2 выполняется равенство нормальных составляющих индукции, то есть:
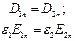 | (3) |
и равенство касательных к поверхности раздела сред напряжённостей электростатического поля:
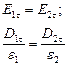 | (4) |
Если силовые линии поля в первой среде имеют с нормалью к поверхности раздела сред угол θ1, а во второй θ2, то линии на границе раздела преломляются с выполнением условия:
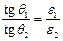 | (5) |
Для металла можно считать, что ε1 = ∞, тогда из (5) следует, что
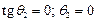 ,
,
то есть силовые линии поля выходят из металла в воздух под углом 900.
Металлическое тело имеет везде одинаковый потенциал.
 При расчёте поля методом интегральных уравнений границу раздела диэлектрик–диэлектрик (воздух) замещают простым слоем зарядов с поверхностной плотностью σ. Найдём связь между вектором напряжённости внешнего поля
При расчёте поля методом интегральных уравнений границу раздела диэлектрик–диэлектрик (воздух) замещают простым слоем зарядов с поверхностной плотностью σ. Найдём связь между вектором напряжённости внешнего поля 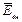 и плотностью простого слоя зарядов. Поскольку
и плотностью простого слоя зарядов. Поскольку 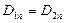 , то
, то

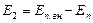
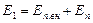
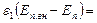
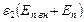

По теореме Гаусса: 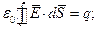
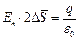 или
или 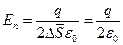
Окончательно получаем:
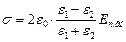 ;
;
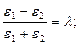
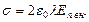
Здесь σ – плотность зарядов, индуцированных на поверхности проводника внешним полем напряженностью 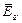 .
.
 2014-02-02
2014-02-02 1068
1068
