Лекция №6
Контрольные вопросы
1. От чего зависит величина ёмкости, как можно увеличить ёмкость?
2. Почему в плоском конденсаторе плотность зарядов на пластинах – величина постоянная?
3. Как можно увеличить ёмкость плоского, цилиндрического и сферического конденсаторов?
4. Определите ёмкость двухпроводной линии, находящейся над землёй.
Методы расчёта электростатических полей.
1. Зеркальный метод изображений и метод Сирла.
2. Решение уравнения Лапласа.
3. Метод интегральных уравнений.
Краткое содержание лекции
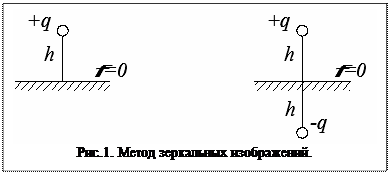 Метод зеркальных изображений является весьма эффективным и в ряде случаев существенно упрощает решение задачи. Пусть заряженное тело находится над проводящим полупространством (в том числе и над Землёй) (рис.1).
Метод зеркальных изображений является весьма эффективным и в ряде случаев существенно упрощает решение задачи. Пусть заряженное тело находится над проводящим полупространством (в том числе и над Землёй) (рис.1).
Идея метода заключается в том, что полупространство убирается и заменяется ещё одним зарядом противоположным по знаку и расположенным по другую сторону границы полупространства. При этом граничные условия на границе раздела воздух-полупространство сохраняются 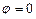 . Затем ведётся расчёт поля двух противоположно заряженных тел.
. Затем ведётся расчёт поля двух противоположно заряженных тел.
Метод зеркальных изображений можно применить и в том случае, когда область расчёта поля представляет собой два полупространства с различными диэлектрическими проницаемостями 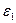 и
и 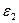 (рис.2)
(рис.2) 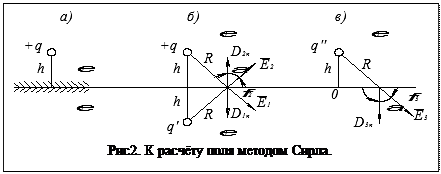 (задача Сирла).
(задача Сирла).
Идея метода Сирла в следующем. В верхней части полупространства поле рассчитывается как поле двух зарядов q и 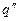 , расположенных в пространстве с диэлектрической проницаемостью
, расположенных в пространстве с диэлектрической проницаемостью 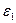 (рис.2.б). В верхней части пространства поле рассчитывается как поле одного заряда
(рис.2.б). В верхней части пространства поле рассчитывается как поле одного заряда 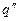 расположенного в пространстве с диэлектрической проницаемостью
расположенного в пространстве с диэлектрической проницаемостью 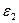 .
.
Поскольку на границе двух сред должны выполняться граничные условия 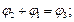
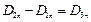 , то можно записать следующее соотношение.
, то можно записать следующее соотношение.
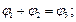
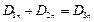
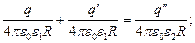
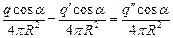
Откуда получаем систему уравнений:
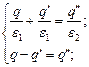
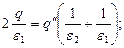
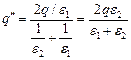 ;
;
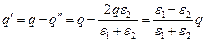
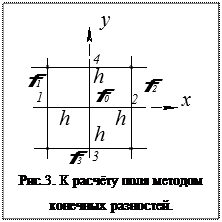 Поскольку расчёт электростатического поля в аналитической форме (то есть в виде формул) удаётся получить в редких случаях, расчёт поля выполняется численными методами. Один из них наистарейших, очень распространённый и проверенный практикой метод конечных разностей. Пространство, в котором ищется решение уравнения Лапласа, разбивается на элементарные площадки (рис.3).
Поскольку расчёт электростатического поля в аналитической форме (то есть в виде формул) удаётся получить в редких случаях, расчёт поля выполняется численными методами. Один из них наистарейших, очень распространённый и проверенный практикой метод конечных разностей. Пространство, в котором ищется решение уравнения Лапласа, разбивается на элементарные площадки (рис.3).
При разбиении области решения на элементарные площадки производные аппроксимируются следующими выражениями:
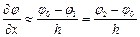
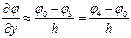
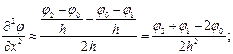
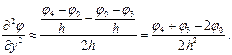
Весь оператор Лапласа заменяется приближённым соотношением:
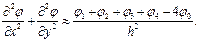
Таким образом, уравнение Лапласа сводится к следующему дискретному уравнению:
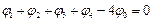
Уравнение Пуассона аппроксимируется выражением:
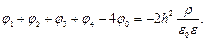
Аппроксимация оператора Лапласа дискретной функцией позволяет свести решение уравнения Лапласа к решению системы линейных алгебраических уравнений.
Метод интегральных уравнений.
Соотношение
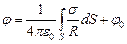 | (1) |
(φ0 – потенциал внешнего источника)
является интегральным уравнением Фредгольма первого рода. Для его численного решения поверхность разбивается на элементарные площадки и (1) превращается в систему линейных уравнений.
Однако система уравнений является плохо обусловленной и для её решения требуются специальные методы, которые называются регуляризацией. Плотность фиктивного слоя зарядов на разделе двух сред с различной диэлектрической проницаемостью равна:
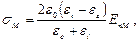 | (2) |
 здесь
здесь 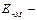 нормальная составляющая напряжённости поля в точке М (рис.4).
нормальная составляющая напряжённости поля в точке М (рис.4).
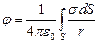 ,
,
поскольку 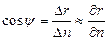
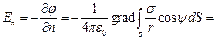
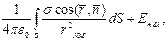 (3)
(3)
где 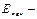 нормальная составляющая от внешних источников электростатического поля. Согласно (2)
нормальная составляющая от внешних источников электростатического поля. Согласно (2)
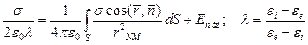
или
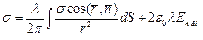 | (4) |
Уравнение (4) называется уравнением Фредгольма второго рода и решается численными методами.
 2014-02-02
2014-02-02 1153
1153








