Лекция №14
Контрольные вопросы
1. Какая электромагнитная волна считается плоской?
2. Выведите уравнение Гельмгольца для напряжённости электрического поля.
3. От каких физических свойств зависит длина волны, которая в нём распространяется?
4. Что такое глубина проникновения электромагнитной волны?
Электромагнитное поле в пластине проводящего магнитного материала.
1. Электромагнитное поле в пластине, по которой распространяется синусоидальный магнитный поток.
2. Комплексная магнитная проницаемость материала пластины.
3. Электромагнитное поле в пластине, по которой протекает синусоидальный ток.
4. Сопротивление пластины переменному току.
 Краткое содержание лекции
Краткое содержание лекции
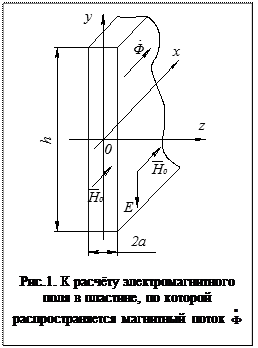
Пусть по пластине (рис. 1) распространяется синусоидальный магнитный поток с комплексным действующим значением 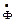 . Найдём распределение электромагнитного поля в пластине. Для напряжённости поля уравнение Гельмгольца имеет вид:
. Найдём распределение электромагнитного поля в пластине. Для напряжённости поля уравнение Гельмгольца имеет вид:
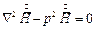
Здесь вектор напряжённости магнитного поля имеет одну составляющую 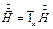 .
.
Поскольку пластина узкая и длинная (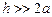 ), напряжённость поля будет зависеть только от одной координаты z, для других координат:
), напряжённость поля будет зависеть только от одной координаты z, для других координат:
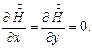
Для данного случая уравнение Гельмгольца сводится к обыкновенному дифференциальному уравнению:
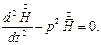
| (1) |
Решением (1) будет функция:
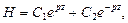
| (2) |
где 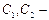 неизвестные комплексные постоянные.
неизвестные комплексные постоянные.
Граничными условиями будут 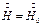 при
при 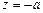 ;
; 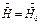 при
при 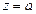 .
.
Используем эти граничные условия для определения С1 и С2.
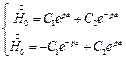
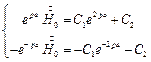
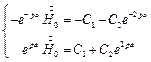
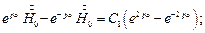
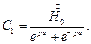
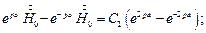
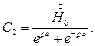
Подставляя 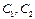 в (2), получаем:
в (2), получаем:
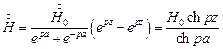 , А/м , А/м
| (3) |
Величина напряжённости электрического поля будет равна:
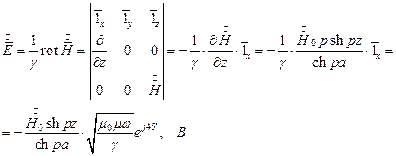
| (4) |
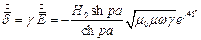 , А/м2
, А/м2
Среднее значение индукции по толщине листа будет равно:
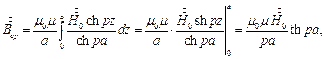
откуда 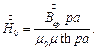
Магнитная проницаемость пластины рассматривается следующим образом:
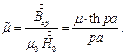
| (5) |
Магнитная проницаемость является комплексным числом 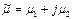 . При сильном поверхностном эффекте (большой частоте, большой проводимости металла) при большом значении Re(pa)
. При сильном поверхностном эффекте (большой частоте, большой проводимости металла) при большом значении Re(pa) 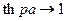 и (5) запишется так:
и (5) запишется так:
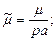
откуда 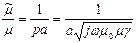 .
.
На единицу площадки пластины приходится поток мощности:
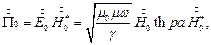
а на единицу объёма:
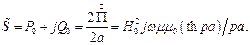
Рассмотрим шину, в которой протекает синусоидальный ток 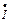 . Поскольку
. Поскольку 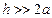 и шина длинная, то напряжённость поля является функцией одной координаты z, при этом
и шина длинная, то напряжённость поля является функцией одной координаты z, при этом 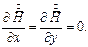
Имеем:
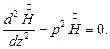
Характеристическое уравнение:
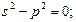
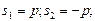
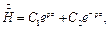
| (6) |
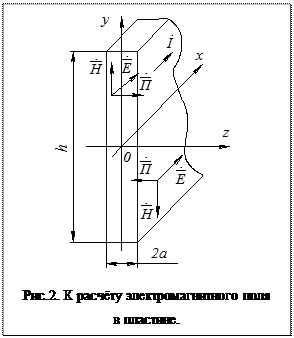 Плотность тока в шине равна:
Плотность тока в шине равна:
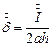
Граничными условиями для уравнения (6) будут:
при 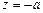
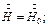
при 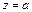
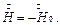
Величину 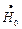 можно найти, используя закон полного тока:
можно найти, используя закон полного тока:
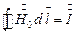 ;
;
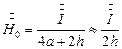 , А/м
, А/м
Используя граничные условия, получаем систему уравнений относительно неизвестных постоянных С1 и С2:
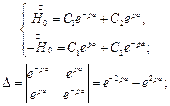
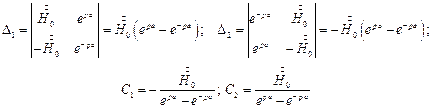
Подставляя значения коэффициентов в (6), получаем:
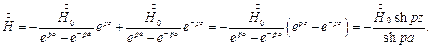
Напряжённость электрического поля:
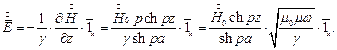
Плотность тока:
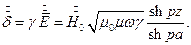
Модули гиперболических функций равны:
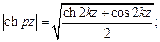
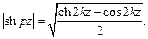
Модули напряжённости магнитного и электрического полей, а также плотности тока равны:
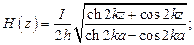
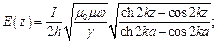
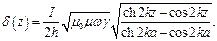
В системах передачи энергии обратным проводом для тока может служить земля.
В энергетических системах переменного тока это, как правило, только аварийный режим. При постоянном токе необходимо считаться сопротивлением в местах растекания тока с заземляющих электродов; на остальном протяжении ток распространяется на столь большое сечение, что сопротивление практически обращается в ноль. Напротив, при переменном токе вследствие поверхностного эффекта поле проникает не слишком глубоко.
Расчет синусоидального электромагнитного поля в цилиндре
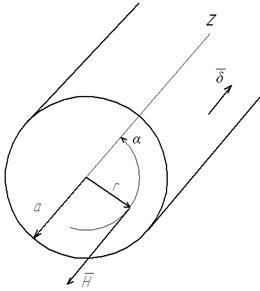 Запишем систему уравнений Максвелла в комплексной форме:
Запишем систему уравнений Максвелла в комплексной форме:
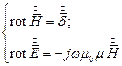
откуда следует:
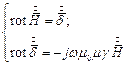
Систему уравнений для вектора плотности тока можно записать так:
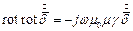 ,
,
или 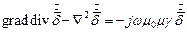 .
.
Поскольку  , то следует:
, то следует:
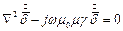
| (7) |
Обозначим 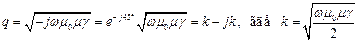 , тогда (7) запишется так:
, тогда (7) запишется так:
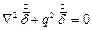 , ,
| (8) |
где 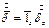 .
.
Поскольку значение вектора 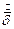 не зависит от z и α, то уравнение (8) превращается в обыкновенное дифференциальное уравнение:
не зависит от z и α, то уравнение (8) превращается в обыкновенное дифференциальное уравнение:
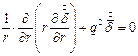 ,
,
или
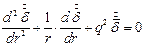 , ,
| (9) |
где 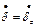 .
.
Обыкновенное дифференциальное уравнение (9) можно привести к виду:
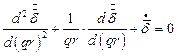 , ,
| (10) |
Уравнение (10) является частным случаем уравнения Бесселя:
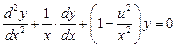 , ,
| (11) |
где u = 0, 1, 2, …
Функции, удовлетворяющие уравнению (11), называются функциями Бесселя. Общий вид функции Бесселя записывается в виде:
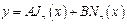 , ,
| (12) |
где А и В – произвольные постоянные; 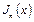 – функция первого рода,
– функция первого рода, 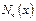 – функция второго рода, n – порядок функции.
– функция второго рода, n – порядок функции.
Уравнение для плотности тока (10) получается из общего уравнения Бесселя, если в нем считать, что n = 0.
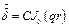 , ,
| (12) |
где 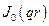 – функция Бесселя первого рода нулевого порядка.
– функция Бесселя первого рода нулевого порядка.
Так как  при r = 0, то она в решение (10) не входит. Если на поверхности цилиндра плотность тока равна, то есть при
при r = 0, то она в решение (10) не входит. Если на поверхности цилиндра плотность тока равна, то есть при 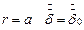 , то:
, то:
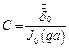 ,
,
и (12) перепишется так:
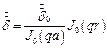 .
.
Напряженность магнитного поля определяется из соотношения:
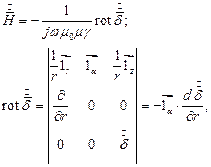
откуда:
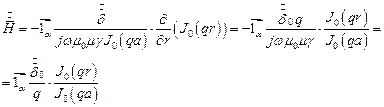
На поверхности цилиндра напряженность равна:
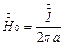
Пусть 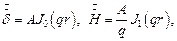 откуда следует:
откуда следует:
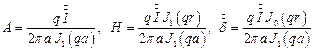
На оси провода 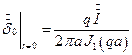 .
.
На поверхности провода 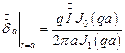 .
.
 2014-02-02
2014-02-02 641
641








