Лекция №13
Контрольные вопросы
1. Почему перед реактивной ёмкостной мощностью появился знак минус?
2. Если мощность передаётся вне проводов, то зачем нужны провода, и можно ли без них обойтись?
3. Как направлен вектор Пойнтинга во внутренней жиле кабеля?
4. Приведите другие примеры расчёта передаваемой мощности.
Электромагнитное синусоидальное поле в проводящем
полупространстве.
1. Плоская электромагнитная волна.
2. Вывод уравнения Гельмгольца.
3. Решение уравнения Гельмгольца для плоской волны.
4. Анализ решения уравнения Гельмгольца.
Краткое содержание лекции
 Если электромагнитная волна распространяется в пространстве и при этом в плоскости имеет одинаковые значения векторов
Если электромагнитная волна распространяется в пространстве и при этом в плоскости имеет одинаковые значения векторов 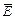 и
и 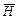 , то такая волна называется плоской.
, то такая волна называется плоской.
Если электромагнитное поле распространяется в проводящем пространстве, то доминирующими становятся токи проводимости, а токами смещения можно пренебречь. Тогда система уравнений Максвелла приобретает вид:
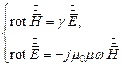
Выразим вектор 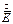 из первого уравнения и подставим его значение во второе уравнение:
из первого уравнения и подставим его значение во второе уравнение:

Получаем:
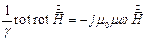
или
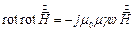 ,
,
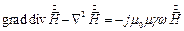
Поскольку 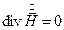 , окончательно получаем:
, окончательно получаем:
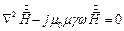
| (1) |
Уравнение (1) называется уравнением Гельмгольца.
Такое же уравнение можно получить относительно вектора напряжённости электрического поля:
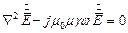
| (2) |
Обозначим 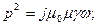
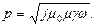
Тогда:
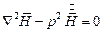
| (3) |
Комплексную величину р можно получить в следующем виде:
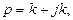 где
где 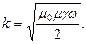
Запишем уравнение (3) в декартовой системе координат, при этом уравнение (3) распадается на три уравнения:
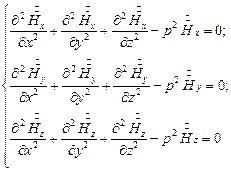
| (4) |
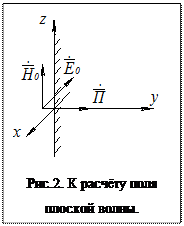 Пусть вектор
Пусть вектор 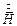 имеет одну составляющую
имеет одну составляющую 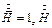 . В полупространстве этот вектор может изменяться только по координате у, а от х и z вектор
. В полупространстве этот вектор может изменяться только по координате у, а от х и z вектор 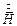 не зависит. То есть имеем плоскую волну. Тогда уравнение из системы уравнений (4) в частных производных превращается в обыкновенное дифференциальное уравнение:
не зависит. То есть имеем плоскую волну. Тогда уравнение из системы уравнений (4) в частных производных превращается в обыкновенное дифференциальное уравнение:
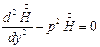
| (5) |
Характеристическим уравнением уравнения (5) будет:
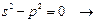
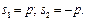
Решение уравнения (5) имеет вид:
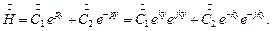
| (6) |
Поскольку у растёт от 0 в положительном направлении, то первое слагаемое в формуле (6) обращается в бесконечность, поэтому оно отбрасывается. В итоге получаем:
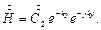
Граничным условием будет: при  . Следовательно,
. Следовательно,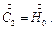 Окончательно запишем:
Окончательно запишем:
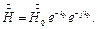
Найдём величину напряжённости электрического поля:
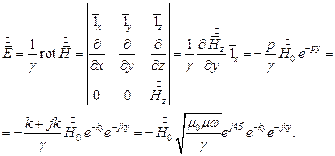
| (7) |
Пусть 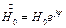 , тогда как функции времени вектора напряжённости магнитного и электрического полей можно записать так:
, тогда как функции времени вектора напряжённости магнитного и электрического полей можно записать так:
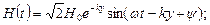 А/м А/м
| (8) |
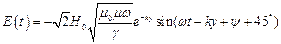 , В/м , В/м
| (9) |
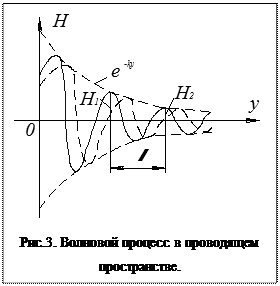
Соотношения (8) и (9) представляют собой волны (рис.3), затухающие с увеличением у:
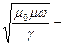 волновое сопротивление.
волновое сопротивление.
Длина волны равна у, при котором волны повторяются.
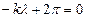
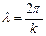
Фазовая скорость движения фазы волны в пространстве, то есть фаза волны должна оставаться неизменной:
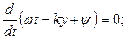

Фазовая скорость равна:
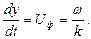
Глубиной проникновения электромагнитной волны в полупространство называется расстояние от поверхности проводящего пространства, при котором амплитуда колебаний уменьшается в 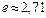 раз:
раз:
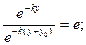
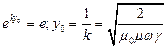 – это глубина проникновения электромагнитной волны в проводящее пространство.
– это глубина проникновения электромагнитной волны в проводящее пространство.
 2014-02-02
2014-02-02 604
604








