Лекция №15
Контрольные вопросы
1. Нарисуйте графики распределения модуля напряжённости магнитного поля по толщине пластины при прохождении по пластине синусоидального потока.
2. Нарисуйте графики распределения модуля напряжённости магнитного поля по толщине пластины при прохождении по пластине синусоидального тока.
3. В чём заключается поверхностный эффект?
4. От каких параметров зависит активное и реактивное сопротивление шины для переменного тока?
Электромагнитное поле в диэлектрике Излучение электромагнитных волн.
1. Вывод уравнения Гельмгольца для диэлектрика.
2. Запаздывающие потенциалы.
3. Уравнение Лоренца.
4. Излучение электрического диполя.
Краткое содержание лекции
В диэлектрике ток смещения намного превосходит ток проводимости, поэтому систему уравнений в комплексной форме Максвелла можно записать в следующем виде:
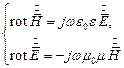
Определяя 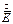 из первого уравнения и подставляя его во второе, получаем:
из первого уравнения и подставляя его во второе, получаем:
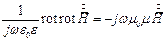
или
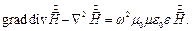
Поскольку 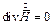 , то получается:
, то получается:
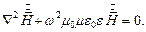
| (1) |
Для вектора напряжённости электрического поля получается аналогичным образом:
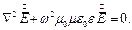
В простейшем случае, когда 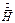 зависит от единственной пространственной координаты
зависит от единственной пространственной координаты 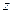 , (1) можно записать как обыкновенное дифференциальное уравнение:
, (1) можно записать как обыкновенное дифференциальное уравнение:
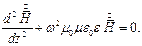
| (2) |
Характеристическое уравнение имеет вид:
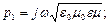
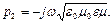
Обозначим 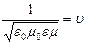 , тогда решением (2) будет:
, тогда решением (2) будет:
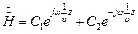
При 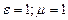 получим
получим 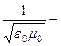 скорость света.
скорость света.
Для плоской волны в полупространстве:
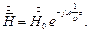
что является незатухающей электромагнитной волной.

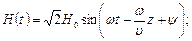
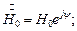
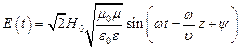
Фазовая скорость волны:
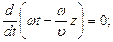
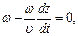 откуда следует
откуда следует 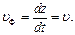
Длина волны 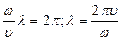
Излучение электромагнитных волн
Обратимся к уравнениям поля, записанным для вакуума:
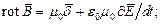
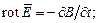
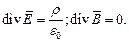
| (3) |
Представим в них основные векторы поля через потенциалы:
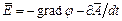 ;
; 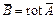
и подставляя их в третье и первое из уравнений (3), получаем:
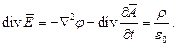
| (4) |
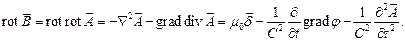
В последнем равенстве целесообразно все слагаемые, содержащие потенциал, перенести в правую часть, после чего оно принимает вид:
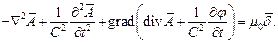
| (5) |
В уравнениях (4) и (5) содержится как скалярный, так и векторный потенциалы. Это крайне неудобно.
При определении векторного потенциала подчёркивается возможность произвольно задаваться значением 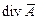 , поскольку
, поскольку 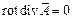 .
.
Как бы не выражалась 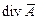 , это не повлияет на
, это не повлияет на 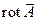 .
.
Принимается для вакуума:
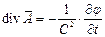
| (6) |
Это калибровка или уравнение Лоренца.
Формулы (4), (5) принимают вид
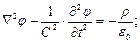
| (7) |
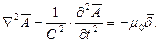
| (8) |
При постоянном поле уравнения (7) и (8) превращаются в уравнение Пуассона.
Решение уравнений (7) и (8) имеет вид:
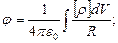 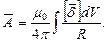
| (9) |
Под интегралами плотность зарядов ρ и плотность тока 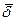 поставлены в квадратные скобки. Это значит, что при интегрировании для получения потенциала в какой-то точке в момент времени
поставлены в квадратные скобки. Это значит, что при интегрировании для получения потенциала в какой-то точке в момент времени 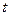 необходимо подставлять заряды и токи, существовавшие в более ранний момент времени, а именно в момент
необходимо подставлять заряды и токи, существовавшие в более ранний момент времени, а именно в момент 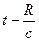 т.е.
т.е. 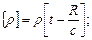
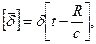 где с – скорость света
где с – скорость света 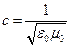 .
.
Потенциалы, выражаемые формулами (9) называются запаздывающими потенциалами.
В сферической системе координат уравнение 7 (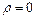 ) запишется так:
) запишется так:
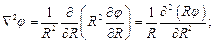
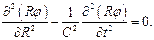
Решение этого уравнения, найденное Даламбером, хорошо известно:
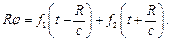
| (10) |
где 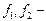 любые функции, удовлетворяющие тем или иным конкретным условиям рассматриваемой задачи. Первая функция в (10)
любые функции, удовлетворяющие тем или иным конкретным условиям рассматриваемой задачи. Первая функция в (10) 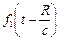 представляет волну, распространяющуюся от начала координат в радиальном направлении со скоростью с. Вторая функция из физических соображений отбрасывается
представляет волну, распространяющуюся от начала координат в радиальном направлении со скоростью с. Вторая функция из физических соображений отбрасывается 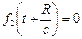 .
.
Итак, получаем зависимость:
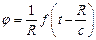 .
.
Решением (10) будет функция:
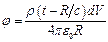
Переходя к интегралу
 , ,
| (11) |
мы получим выражение для запаздывающего потенциала.
 2014-02-02
2014-02-02 430
430







