На примере оператора Лапласа

Основные свойства операторных преобразований,

-

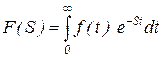Требования функции f(t):

1) эта функция f(t) = 0 при t < 0.

2) функция f(t) = 0 непрерывна и кусочно дифференцируема при t ≥ 0.

3) функция f(t) = 0 ограничена по величине: f(t) ≤ |Me ^e+|

4 основных свойства операторных преобразований:

1) Если увеличить оригинал в а раз, то и изображение увеличится в а раз:

а · f(t) ÷> а ·F(S)

2) Сумма оригиналов равна сумме изображений: f₁(t) + f₂(t)→ F₁(S) + F₂(S)

3) Дифференцирование оригинала равнозначно умножению изображения на соответствующий оператор:

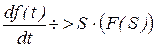
4) Интегрирование оригинала равнозначно делению изображения на соответствующий оператор:

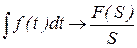
Два последних свойства показывают, что действия дифференцирования и интегрирования оригиналов превращаются в действия умножения и деления их изображений. Таким образом дифференциальные уравнения функций действительных переменных превращаются в алгебраические уравнения для их изображений. Общая последовательность использования операторного метода включает:

1) составление дифференциального уравнения движения системы в функциях действительной переменной времени;

2) выполнение операторного перехода, связанного с нахождением соответствующих изображений и получение алгебраического уравнения, описывающего поведение системы в функциях изображений;

3) решение получившегося алгебраического уравнения и нахождение изображения искомой функции;

4) обратный операторный переход с помощью таблиц преобразований и нахождение по изображению функции ее оригинала. Найденная функция – оригинал будет решением уравнения движения системы.