xвыx(t) ÷> Xвыx(S)
xвx(t) ÷> Xвx(S)
f(t) ÷> F(S)
aoSnXвыx(S) + a1Sn-1Xвыx(S) + … + anXвыx(S)=
= boSmXвx(S) + b1Sm-1Xвx(S) + … + bmXвx(S) + coS·F(S) + c1F(S) (3.5)
Уравнение движения в операторной форме.
Группируем Q(S)
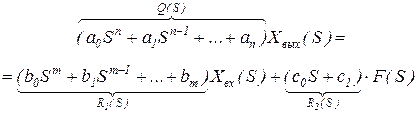 (3.6)
(3.6)
Q(S) – характеристический полином (собственный оператор системы)
R1 – операторы воздействия (по входному сигналу)
R2 – операторы воздействия (по внешнему возмущению)
Q(S)· Xвыx(S) = R1(S) Xвx(S) + R2(S)·F(S) |: Q(S)
Xвыx(S) = 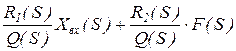
Отношение оператора воздействия к собственному оператору называется передаточной функцией системы по данному воздействию W(S):
Xвыx(S) = W1(S) · Xвx(S) + W2(S)·F(S) (3.7)
Выражение (3.7) отражает важнейший принцип работы линейных систем автоматического управления, которые называется принципом суперпозиции: реакция системы на несколько внешних возмущений равновесия сумме ее реакций на каждое из возмущений в отдельности.
W1(S) = 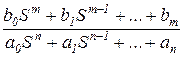 (3.8)
(3.8)
S ≡ 0 (при отсутствии изменений)
W1(0) = 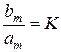 – передаточный коэффициент системы.
– передаточный коэффициент системы.
 2014-02-02
2014-02-02 1382
1382








