Непрерывность функции. О-более высокого порядка малости

О-более высокого порядка малости

Док-во: 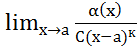=1→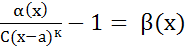

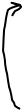
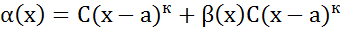(обе части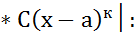

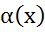
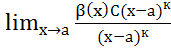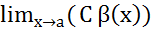=числитель более высокого порядка малости чем знаменатель

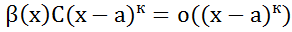
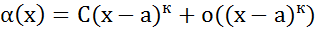чтд

Прим1.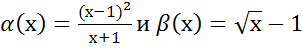беск малые при х→1

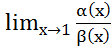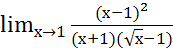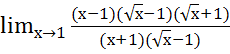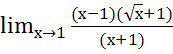=== =0 вывод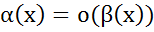

Прим2.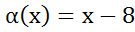;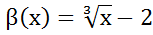беск малые при х→8

==

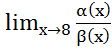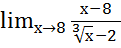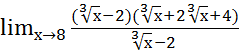
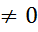=12вывод 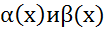наз величинами одного порядка малости.

Прим3 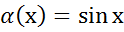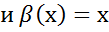беск малые при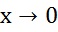

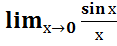=1 - первый замечательный предел

Опр. f: (а,в)→𝑅 наз непрерывной в т.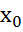если 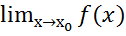равен значению ф в этой точке,те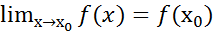

f: (а,в)→𝑅наз непрерывной на мн-ве (а,в) если она непрерывна в каждой т. этого мн-а

Теор:арифметические св-ва непрерывных ф-ий

Пусть f: (a,b)→𝑅 g: (a,b)→𝑅 непрерывные ф в т.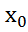⊂мн-ву (а,в), тогда f(x)+g(x), f(x)g(x),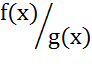непрерывны в т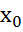

Док-во: f(x)g(x) непрерывны в т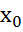,где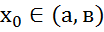

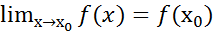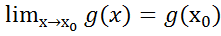,,тогда по т.об арифм операциях над пределами 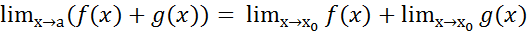=aнепрерывна

=

=

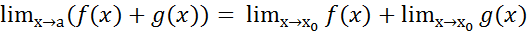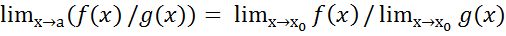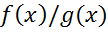
Теор:о непрерывности сложной ф-ции

Пусть у→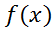непрерывна а в т.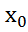; 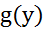непрерывна в т.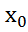,тогда сложная ф 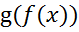непрерывна в т.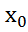

Зам-ие:все элементарные ф-ции вкл обратные тригонометрические и гиперболические непрерывны в т.,в которой опред их значения

Пр1.у=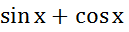непрерывна для любого х как сумма 2х ф

Пр2.у=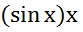непрерывна для любого х как произв 2х ф

Пр3.у=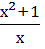непрерывна во всех т кроме х=0 как частное 2х ф

Пр4у=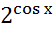непрерывна как сложн ф 2х непрерывных ф