Во многих случаях введение новой переменной интегрирования позволяет свести данный интеграл к более простому. Такой метод называется методом замены переменной или методом подстановки.
Пусть функция 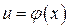 непрерывно дифференцируема на промежутке и имеет обратную функцию
непрерывно дифференцируема на промежутке и имеет обратную функцию 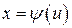 . Тогда
. Тогда
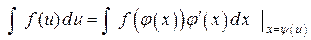 .
.
При замене переменной в интеграле 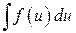 нужно
нужно
а) заменить переменную 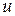 на функцию
на функцию 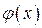 , заменить
, заменить 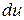 на
на 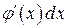 ,
,
б) вычислить получившийся интеграл,
в) результат выразить через первоначальную переменную 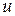 .
.
Пример 1. Найти 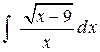 . Это − интеграл типа
. Это − интеграл типа 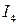 .
.
В соответствии с рекомендацией сделаем замену 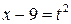 . Тогда
. Тогда 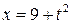 ,
, 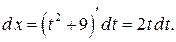 Подставим выражения для
Подставим выражения для 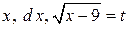 в интеграл:
в интеграл:
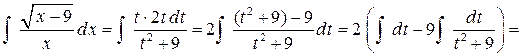
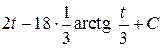 .
.
Получившийся результат надо выразить через переменную  . Учитывая, что
. Учитывая, что 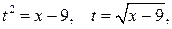 получим
получим
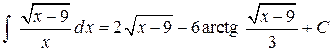 .
.
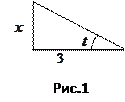 Пример 2. Найти
Пример 2. Найти 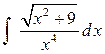 . Это − интеграл типа
. Это − интеграл типа 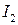 .
.
В соответствии с рекомендацией сделаем замену 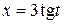 . Тогда
. Тогда
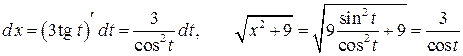 .
.
Подставляя выражения для 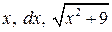 в интеграл, получим
в интеграл, получим
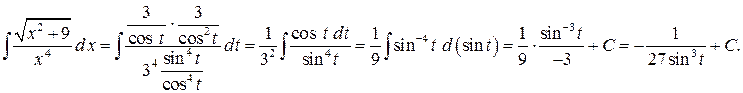 Получившийся результат надо выразить через переменную
Получившийся результат надо выразить через переменную  , учитывая, что
, учитывая, что 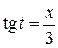 . Удобно воспользоваться прямоугольным треугольником с углом t, противолежащим катетом
. Удобно воспользоваться прямоугольным треугольником с углом t, противолежащим катетом  и прилежащим катетом, равным 3 (рис. 1). Тогда
и прилежащим катетом, равным 3 (рис. 1). Тогда
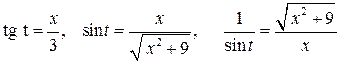 и
и 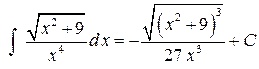 .
.
Пример 3. Найти 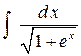 .
.
Сделаем замену переменной 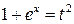 . Тогда
. Тогда 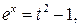
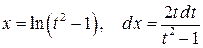 ,
,
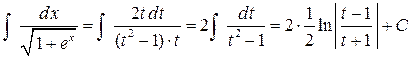 .
.
Подставляя 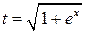 , получим
, получим 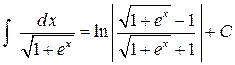 .
.
 2014-02-02
2014-02-02 923
923








