Метод подведения под знак дифференциала

Этот метод применяется для вычисления интегралов вида . Воспользуемся тем, что 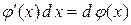. При этом говорят, что мы подвели функцию 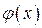под знак дифференциала. Если еще сделать замену 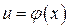, то мы получим интеграл более простой, чем первоначальный:

.

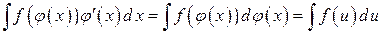После нахождения этого интеграла следует вернуться к переменной , заменив 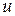на .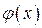

Отметим, что при подведении функции под знак дифференциала, прежде всего, используется определение дифференциала и два его свойства

,

.

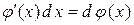
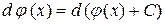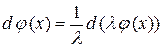
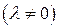Рассмотрим, как подвести под знак дифференциала некоторые функции:

, ,

, ,

, ,

, .

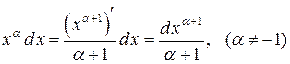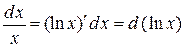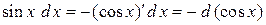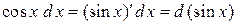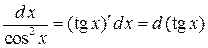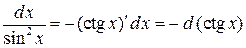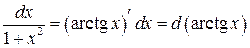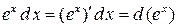Список таких формул можно продолжить. Важно понять, как они получаются.

Рассмотрим примеры на вычисление неопределенных интегралов методом подведения под знак дифференциала.